十大排序算法的数组和链表实现

数组排序在牛客,进行测试；链表排序在leetcode进行测试。

发现一个牛逼的数据结构与算法的可视化网站(https://visualgo.net/zh)
链表定义：

Definition for singly-linked list.
struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};

概述

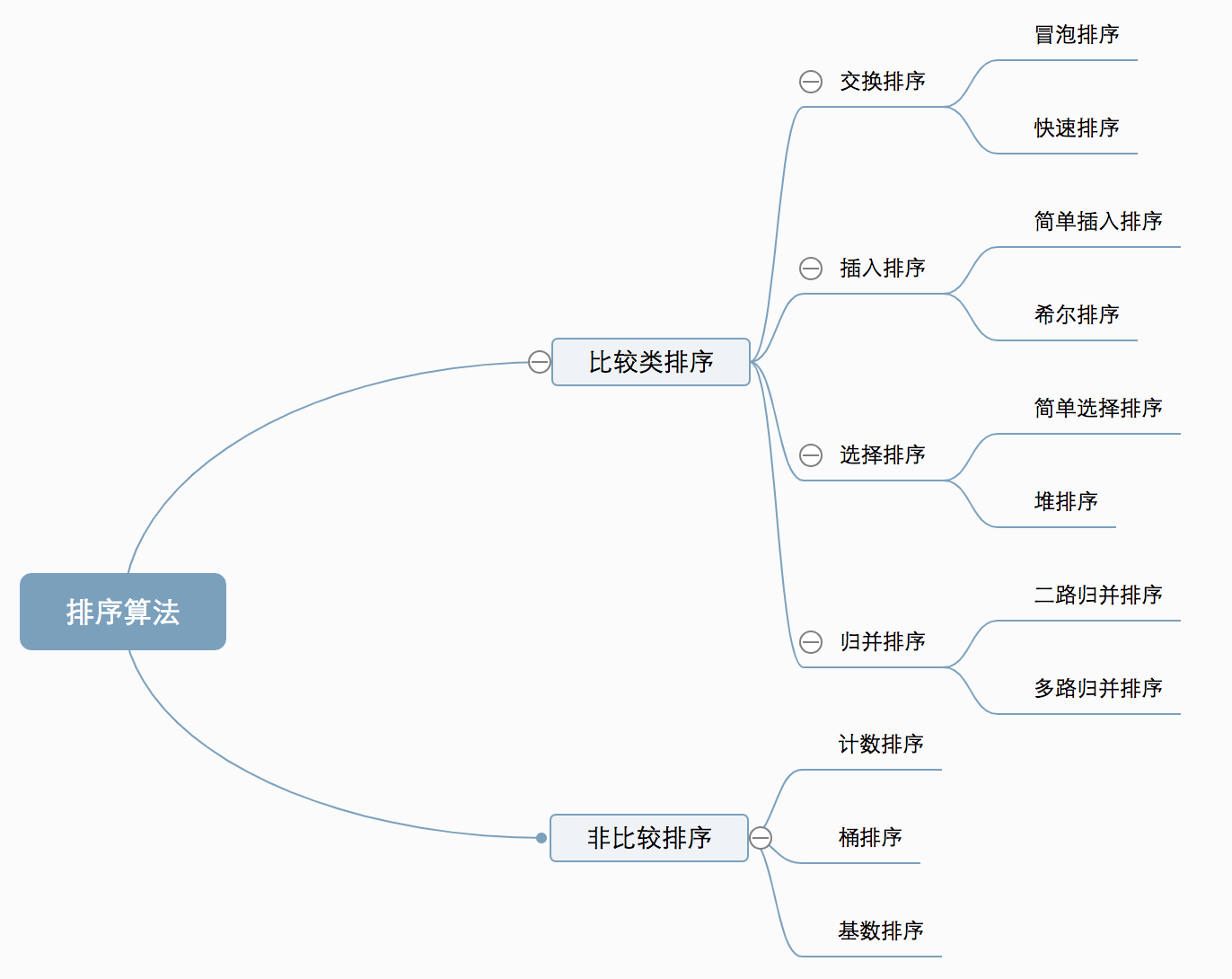
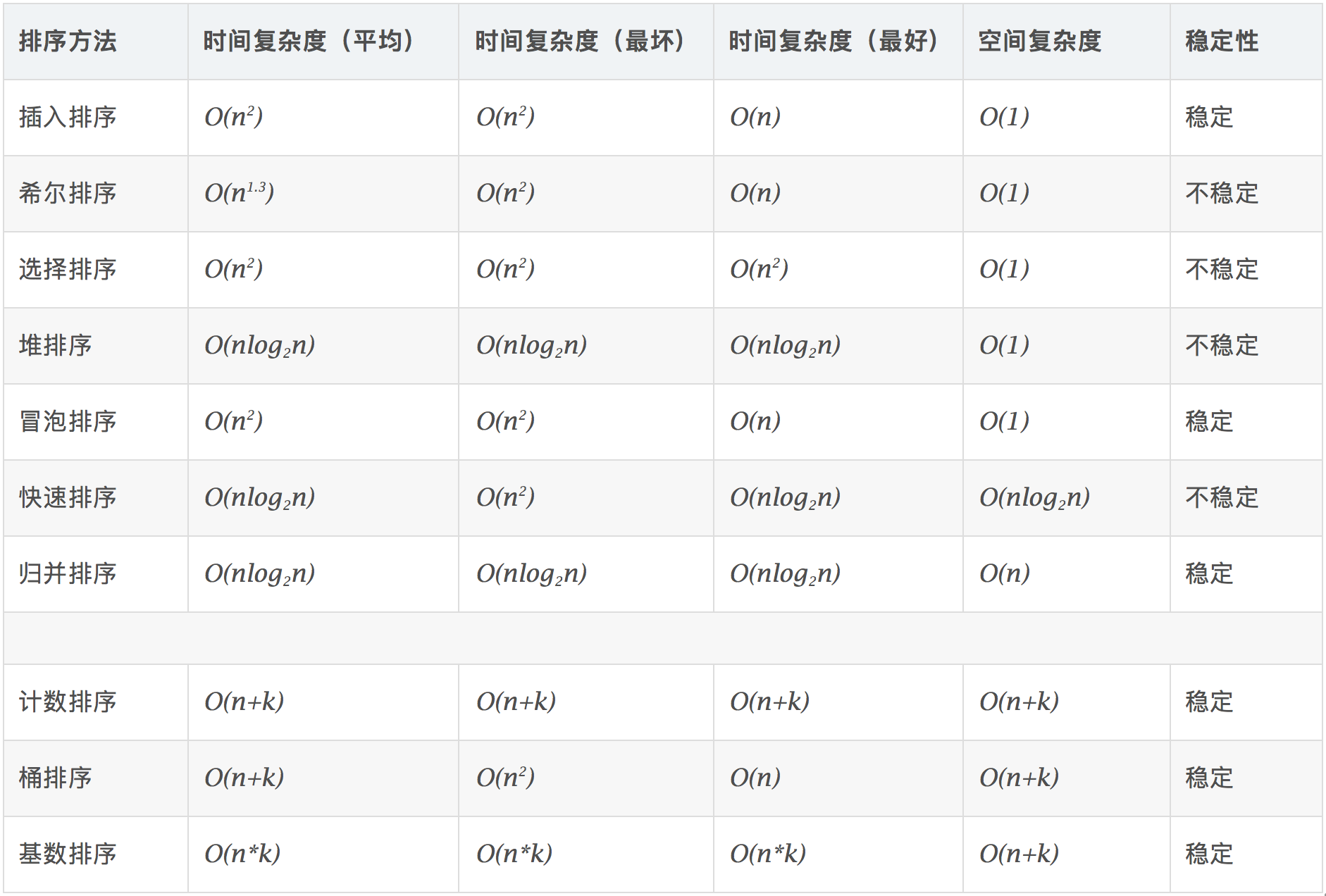
相关概念

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
• 不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
• 时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。
• 空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。

1. 冒泡排序（Bubble Sort）

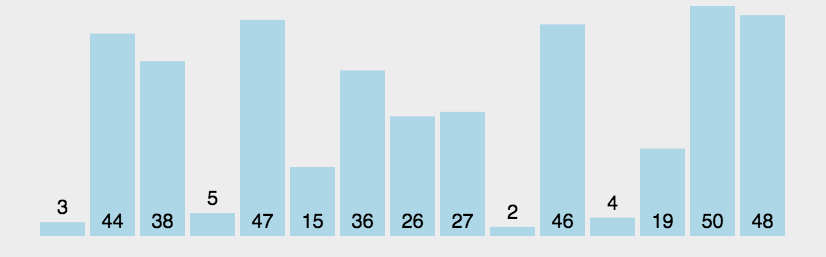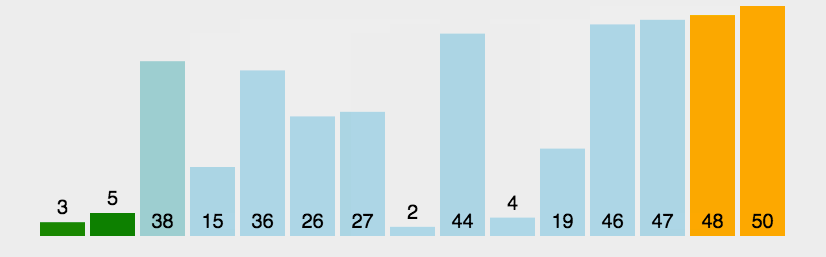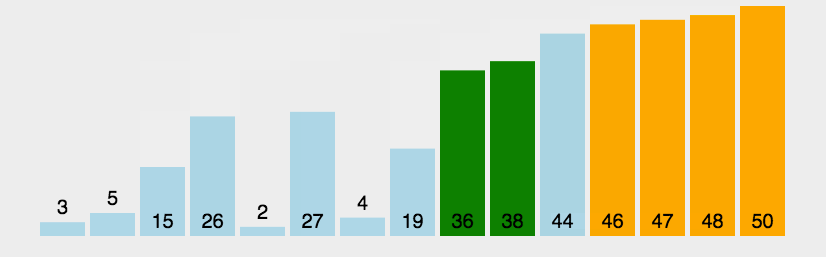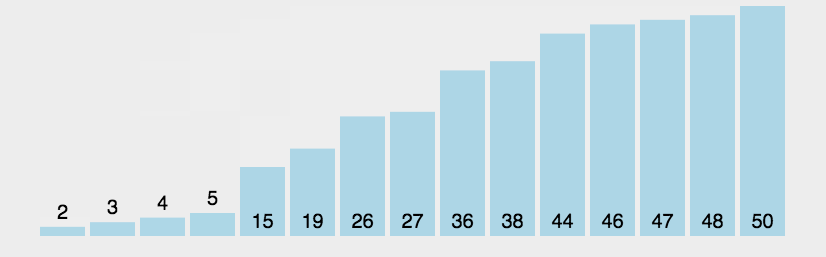
• 平均时间复杂度$O(N^{2})$
• 空间复杂度$O(1)$
• 稳定

数组

#include <bits/stdc++.h>
using namespace std;
//注意：本算法排序要求链表在2个及以上，暂未加入对于0 1个数的排序；数组不能为空
//newoder pass
array
int main(){
   ios::sync_with_stdio(0);
   cin.tie(0);
   int tmp = 0;
   vector<int> a;
   cin>>tmp;
   a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
   while(true){
       if(cin.get()=='\n') break;
       cin>>tmp;
       a.push_back(tmp);
   }

   bool isChange = true;//标志位用来标记这一轮是否进行过交换，未交换说明数组已经有序
   int n = a.size();
   for(int i=0; i<n-1; i++){
       if(!isChange) break;
       isChange = false;
       for(int j=0; j<n-i-1;j++){
           if(a[j] > a[j+1]){
//                int tmp = a[j+1];
//                a[j+1] = a[j];
//                a[j] = tmp;
               swap(a[j],a[j+1]);
               isChange = true;
           }
       }
   }

   for(const int &e:a){
       cout<<e<<' ';
   }
   cout<<'\n';
}

链表
交换val的值

class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        if(!head || !head->next) return head;
        ListNode *dummy = new ListNode(0);
        dummy->next = head;
        auto cur = dummy->next;
        bool isChange = true;//标志位用来标记这一轮是否进行过交换，未交换说明数组已经有序
        ListNode *tail = nullptr;//冒泡的范围是[head,tail)，head就是cur
        while(tail != cur->next && isChange){//若尾部指针tail没到第二位，继续冒泡
            ListNode *p = cur;//p从cur开始
            isChange = false;
            for(;p->next != tail; p = p->next){//从前往后，直到tail
                if(p->val > p->next->val){
                swap(p->val, p->next->val);
                isChange = true;
                }
            }
        }
        return dummy->next;
    }
};

2. 选择排序（Selection Sort）

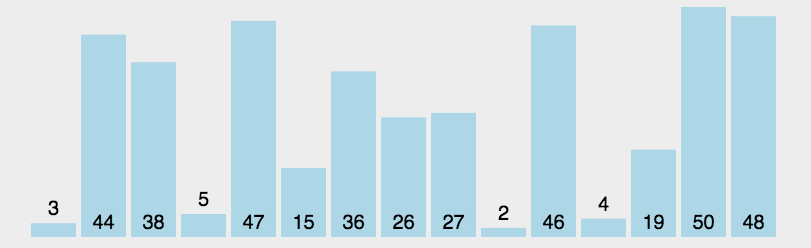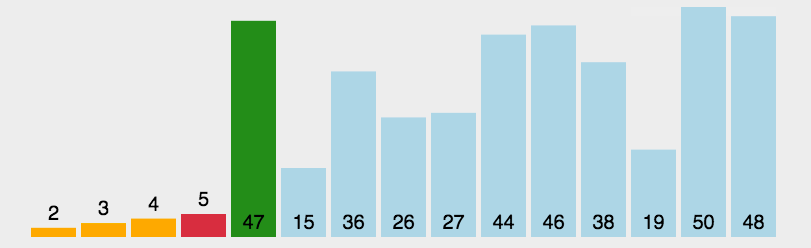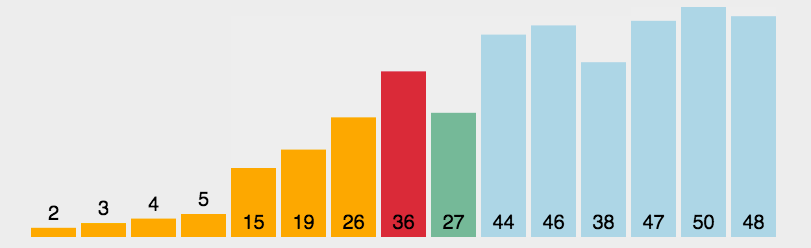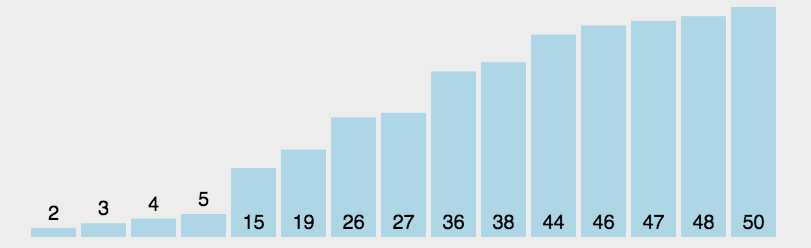
• 平均时间复杂度$O(N^{2})$
• 空间复杂度$O(1)$
• 不稳定

数组

#include <bits/stdc++.h>
using namespace std;
////注意：数组不能为空
//array
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int tmp = 0;
    vector<int> a;
    int n = 0;
    cin>>n;
    cin>>tmp;
    a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
    while(true){
        if(cin.get()=='\n') break;
        cin>>tmp;
        a.push_back(tmp);
    }

    for(int i=0; i<a.size()-1; i++){
        int min_index = i;
        for(int j=i+1; j<a.size(); j++){
            if(a[j] < a[min_index]) min_index = j;
        }
        if(min_index != i) swap(a[i],a[min_index]);
    }

    for(const int &e:a){
        cout<<e<<' ';
    }
    cout<<'\n';
}

链表
交换val的值

占坑

3. 插入排序（Insertion Sort）

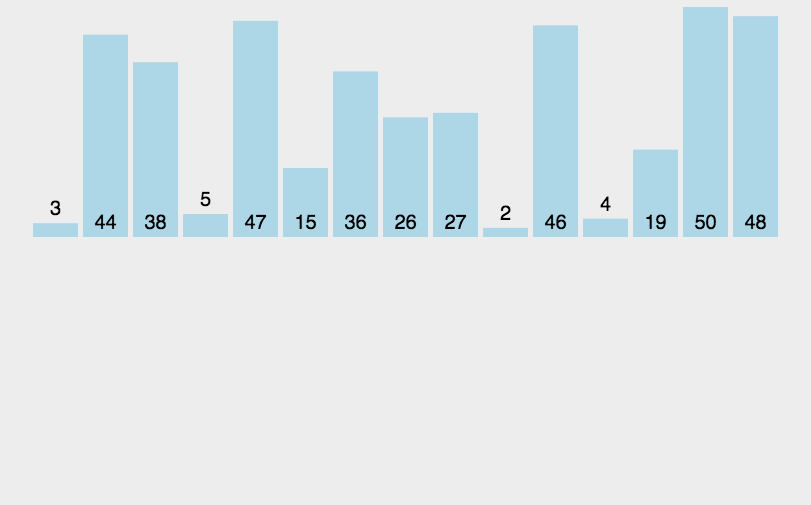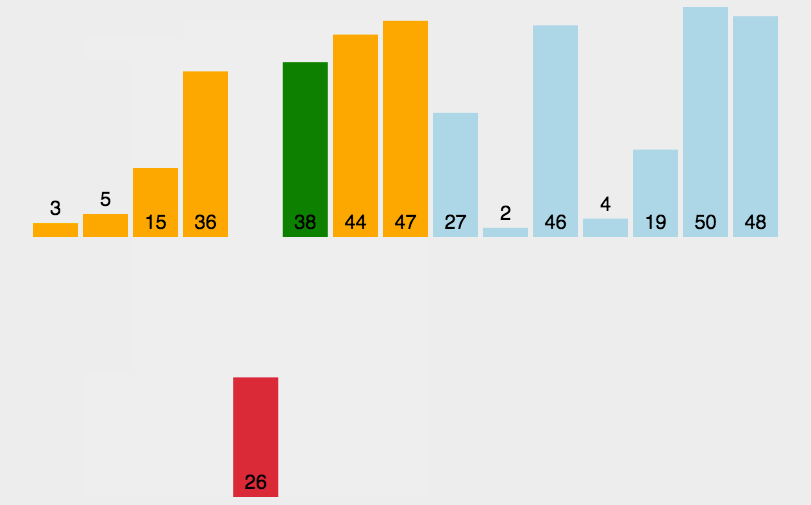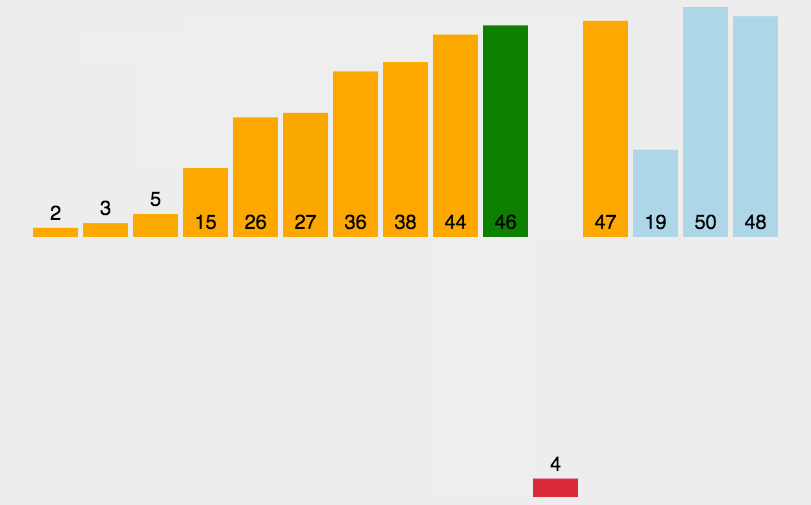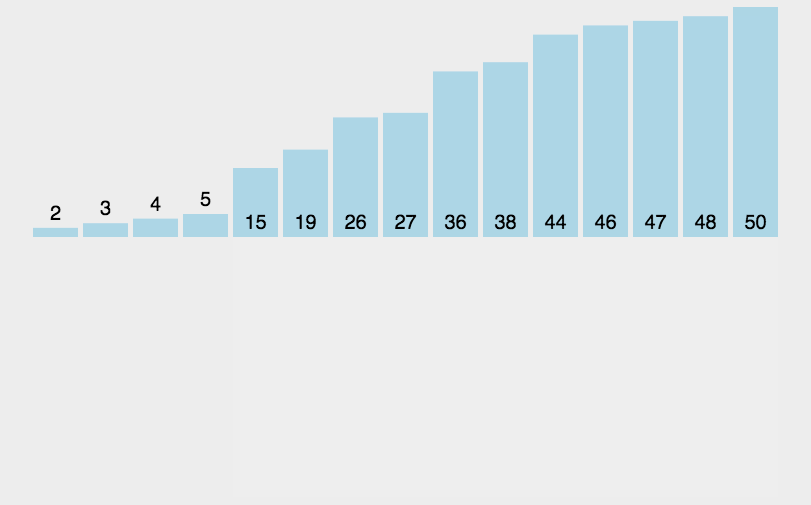
• 平均时间复杂度$O(N^{2})$
• 空间复杂度$O(1)$
• 稳定

数组

#include <bits/stdc++.h>
using namespace std;
////注意：数组不能为空
////nowcoder pass
//array
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int tmp = 0;
    vector<int> a;
    cin>>tmp;
    a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
    while(true){
        if(cin.get()=='\n') break;
        cin>>tmp;
        a.push_back(tmp);
    }

    for(int i=1; i<a.size(); ++i){//有序区的长度依次递增，范围为[0,i)
        for(int j=i; j>0; --j){//从i开始往前挨个比较
            if(a[j] < a[j-1]) swap(a[j],a[j-1]);//若小就
            else break;
        }
    }

    for(const int &e:a){
        cout<<e<<' ';
    }
    cout<<'\n';
}

链表
交换节点

占坑

4. 希尔排序（Shell Sort）

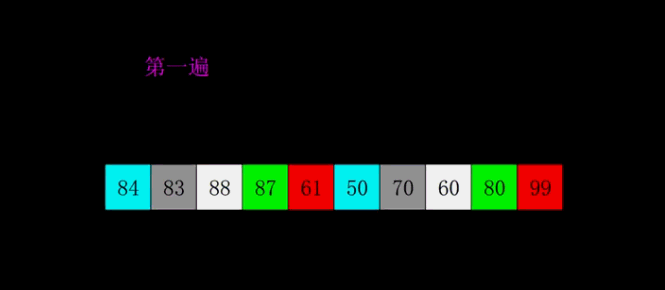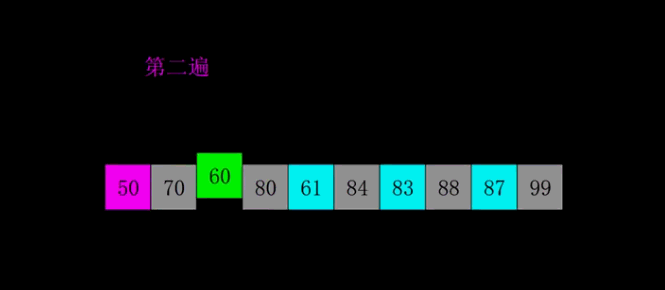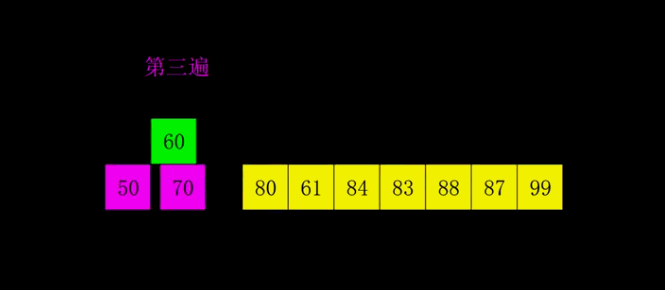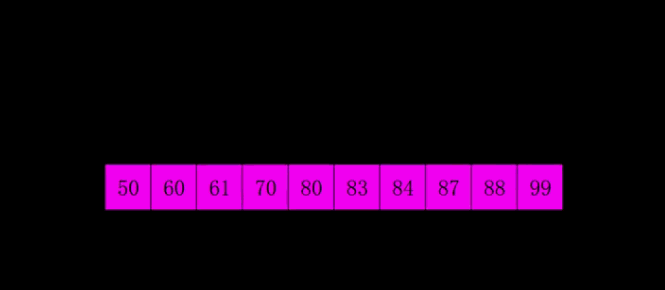
• 平均时间复杂度$O(N^{1.3})$
• 空间复杂度$O(1)$
• 不稳定

数组

#include <bits/stdc++.h>
using namespace std;
////注意：数组不能为空
///nowcoder pass
//array
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int tmp = 0;
    vector<int> a;
    int n = 0;
    cin>>n;//这个是nowcoder会用到的一个n，用来记录数组长度
    cin>>tmp;
    a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
    while(true){
        if(cin.get()=='\n') break;
        cin>>tmp;
        a.push_back(tmp);
    }

    n = a.size();
    int dis = n/2;//设置步长，保证小于n，且最后能迭代到1就行，如dis/3-1
    while(dis>=1){//缩短到dis=1停止
        for(int i=dis; i<n; i++){//通过dis选择比较的第二个数的位置
            for(int j=i-dis; j>=0; j -= dis){//注意j-dis若>=0，继续比较
                if(a[j] > a[j+dis]) swap(a[j], a[j+dis]);
            }
        }
        dis /= 2;//全部交换完成，dis减小，此处应该和dis定义处相同，即可以为dis/3-1
    }


    for(const int &e:a){
        cout<<e<<' ';
    }
    cout<<'\n';
}

链表

对于希尔排序，因为排序过程中经常涉及到a[i+dis]操作，其中dis为希尔排序的当前步长，这种操作不适合链表。

5. 堆排序（Heap Sort）

• 平均时间复杂度$O(Nlog{N})$
• 空间复杂度$O(1)$
• 不稳定

数组

#include <bits/stdc++.h>
using namespace std;
////注意：数组不能为空
///nowcoder pass
//array

void heapify(vector<int>& a, int father, int end){
    int son = father*2+1;
    while(son<end){
        if(son+1 < end && a[son] < a[son+1]) son++;//取两个子节点里面大的
        if(a[father] > a[son]) break;//若father>son，说明三个数里面最大的数已经在顶上
        else{
            swap(a[father],a[son]);
            father = son;//变化的son变为father继续取最大
            son = son*2+1;
        }
    }
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int tmp = 0;
    vector<int> a;
    int n = 0;
    cin>>n;//这个是nowcoder会用到的一个n，用来记录数组长度
    cin>>tmp;
    a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
    while(true){
        if(cin.get()=='\n') break;
        cin>>tmp;
        a.push_back(tmp);
    }

    n = a.size();
    for(int i=n/2+1; i>=0; i--){//最后一个父节点是从n/2+1开始，从这个节点往前迭代建立第一个堆
        heapify(a, i, n);
    }
    for(int i=n-1; i>0; --i){
        swap(a[0], a[i]);//取堆顶的最大值，放到数组最后
        heapify(a, 0, i);//这次只调整最大的堆顶就可以，因为其他父节点已经有序
    }


    for(const int &e:a){
        cout<<e<<' ';
    }
    cout<<'\n';
}

链表

堆排序也经常会有跨越多个节点找子节点的情况，因此不适合链表。
也可以用二叉树实现，但需要额外空间，比较复杂。

6. 归并排序（Merge Sort）

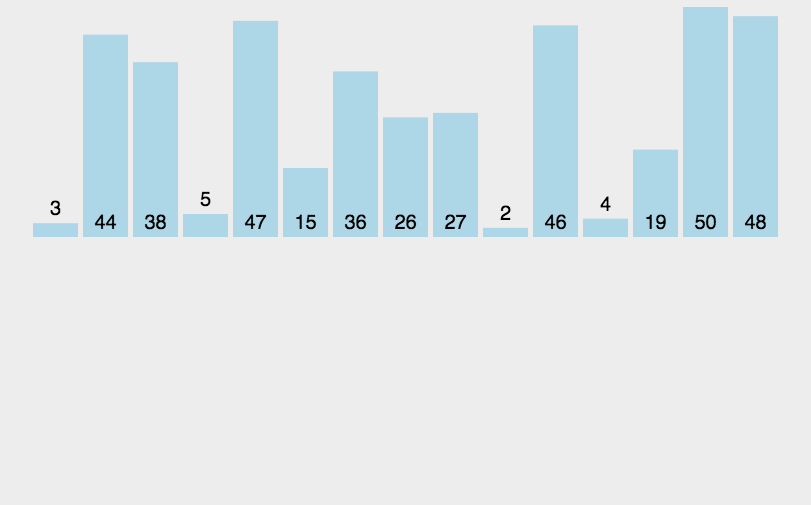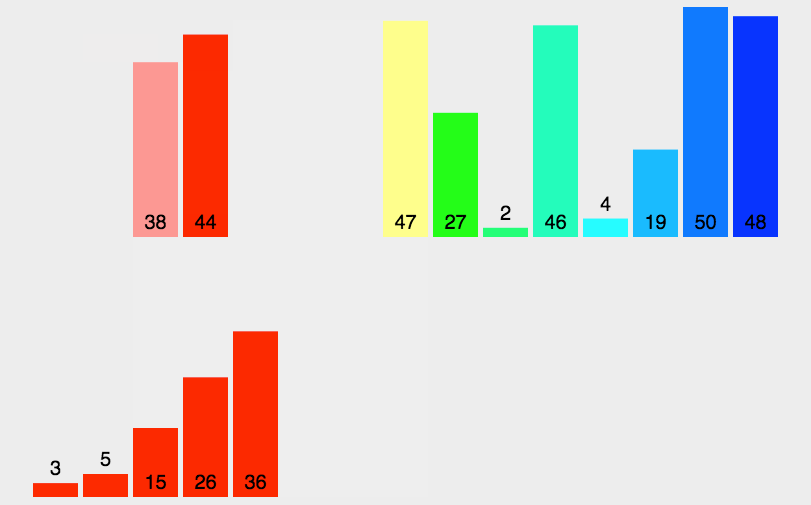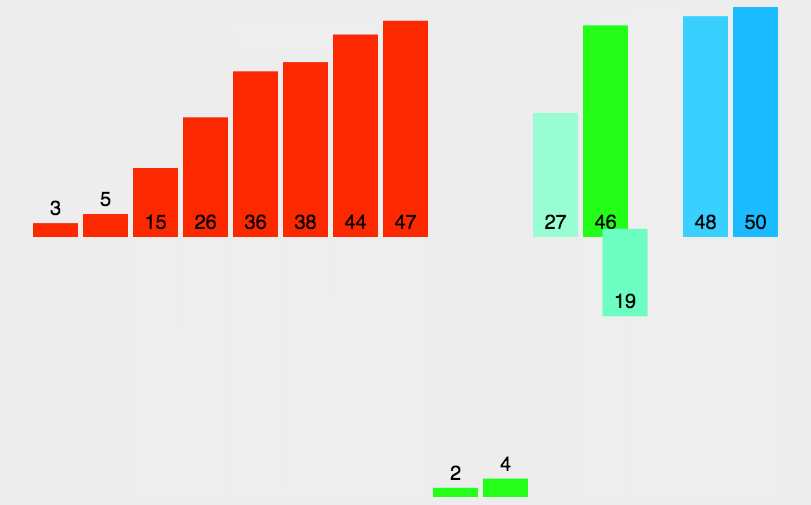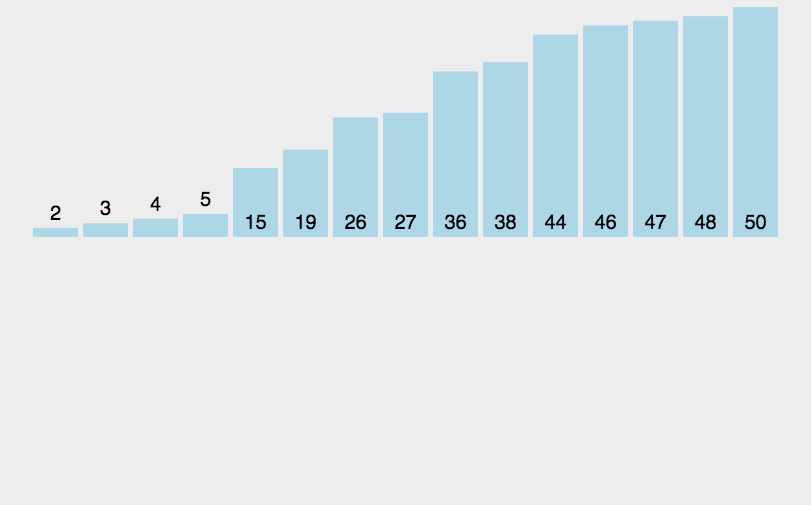
• 平均时间复杂度$O(Nlog{N})$
• 空间复杂度$O(N)$(非递归法); $O(N+log{N})$(递归法)
• 稳定

数组
递归

#include <bits/stdc++.h>
using namespace std;
////注意：数组不能为空
///nowcoder pass
//array
//递归
void Merge(vector<int>& a, vector<int> &b, int start1, int end1, int start2, int end2){
    int b_start = start1;//定义b开始位置的指针
    int tmp_start = start1;
    while(start1 <= end1 && start2 <= end2){
        b[b_start++] = a[start1] < a[start2]? a[start1++]:a[start2++];//取两序列比较中小的值
    }
    while(start1 <= end1) b[b_start++] = (a[start1++]);
    while(start2 <= end2) b[b_start++] = (a[start2++]);//会有一个序列还剩一些数，接到b后面

    //在b中排好序再放入a中
    for(int i=tmp_start; i<=end2; i++){
        a[i] = b[i];
    }
}

void MergeSort(vector<int>& a, vector<int>& b, int start, int end){
    if(start >= end) return;//递归终止条件
    int mid = (end-start)/2 + start;//计算中间值
    int start1 = start, end1 = mid;
    int start2 = mid+1, end2 = end;//把数组分成两部分

    MergeSort(a, b, start1, end1);
    MergeSort(a, b, start2, end2);//两部分分别归并
    Merge(a, b, start1, end1, start2, end2);

}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int tmp = 0;
    vector<int> a;
    int n = 0;
    cin>>n;//这个是nowcoder会用到的一个n，用来记录数组长度
    cin>>tmp;
    a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
    while(true){
        if(cin.get()=='\n') break;
        cin>>tmp;
        a.push_back(tmp);
    }

    n = a.size();//a是原始数组
    vector<int> b(n);//b是用来辅助排序的数组
    MergeSort(a,b,0,n-1);


    for(const int &e:a){
        cout<<e<<' ';
    }
    cout<<'\n';
}

非递归

#include <bits/stdc++.h>
using namespace std;
////注意：数组不能为空
///nowcoder pass
//array
//非递归
void Merge(vector<int>& a, vector<int> &b, int start1, int end1, int start2, int end2){
    int b_start = start1;
    int tmp_start = start1;
    while(start1 <= end1 && start2 <= end2){
        b[b_start++] = a[start1] < a[start2]? a[start1++]:a[start2++];//取两序列比较中小的值
    }
    while(start1 <= end1) b[b_start++] = (a[start1++]);
    while(start2 <= end2) b[b_start++] = (a[start2++]);//会有一个序列还剩一些数，接到b后面

    for(int i=tmp_start; i<=end2; i++){
        a[i] = b[i];
    }
}
//主要区别在于这一部分不使用递归实现了
void MergeSort(vector<int>& a, vector<int>& b, int start, int end){
    int n = end-start+1;//n是数组的长度
    //从下向上，先1个1个，再2个2个，最后到stride为n，进行归并
    for(int stride = 1;stride <= n; stride *= 2){
        int i = start;
        //按stride为步长进行两两归并，当数组剩下的数少于2*stride时停止
        for(; i<=end-2*stride+1; i += 2*stride){
            Merge(a, b, i, i+stride-1, i+stride, i+2*stride-1);
        }
        //看剩下的数够不够1个stride，够的话就再归并一次，即使两个数组长度可能不一样
        if(i < end-stride+1){
            Merge(a, b, i, i+stride-1, i+stride, end);
        }
    }




}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int tmp = 0;
    vector<int> a;
    int n = 0;
    cin>>n;//这个是nowcoder会用到的一个n，用来记录数组长度
    cin>>tmp;
    a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
    while(true){
        if(cin.get()=='\n') break;
        cin>>tmp;
        a.push_back(tmp);
    }

    n = a.size();
    vector<int> b(n);
    MergeSort(a,b,0,n-1);


    for(const int &e:a){
        cout<<e<<' ';
    }
    cout<<'\n';
}

链表
递归

class Solution {//用归并排序，且不能用递归（因为递归会用到栈，会用到O(n)级别的空间复杂度）
                //但是写个递归练练手，正确答案看第一个提交结果，merge直接用双路归并merge。递归方法不用cut，各种边界条件还得记记
public:
    ListNode* sortList(ListNode* head) {//递归方法不用哑节点，另一种方法需要
        if(!head || !head->next) return head;//当只有0-1个数时，直接返回该链表，不用排序
        auto *slow = head, *fast = head, *pre = head;
        //三个指针，slow，fast用于找终点，pre指向中点前一个节点，slow指向中点后一个节点
        //注意这里中点是靠前的一个，奇数个节点fast指向最后一个数，偶数个节点fast指向nullptr
        while(fast && fast->next){//注意这种前进两个指针fast的需要判断两个值
            pre = slow;
            slow = slow->next;
            fast = fast->next->next;
        }
        pre->next = nullptr;//断开链表
        return merge(sortList(head),sortList(slow));//调用递归双路归并
    }

    ListNode* merge(ListNode* l1, ListNode* l2){//双路归并
        auto DummyHead = new ListNode(-1);//哑节点
        auto cur = DummyHead;//注意这里哑节点先不加入链表，用于创建新链表
        while(l1 && l2){
            if(l1->val < l2->val){
                cur->next = l1;
                l1 = l1->next;
            }
            else{
                cur->next = l2;
                l2 = l2->next;
            }//哪个小接哪个
            cur = cur->next;//cur指针后移一位
        }
        cur->next = l1? l1:l2;//一条链遍历完成另一条可能还有剩余，因此判断哪条有剩并接上
        return DummyHead->next;
    }
};

非递归
leetcode#148里提到使用栈会使用额外的空间，空间复杂度不为常数，因此应该使用迭代

/*迭代写法*/
class Solution {//用归并排序，且不能用递归（因为递归会用到栈，会用到O(n)级别的空间复杂度）
                //两个重要函数
                //双路归并(merge)：挨个比较两链表的节点大小，哪个小(大)取哪个接在新链表后面
                //断链(cut)：将链表 l 切掉前 n 个节点，并返回后半部分的链表头。
public:
    ListNode* sortList(ListNode* head) {
        auto DummyHead = new ListNode(-1);//哑节点
        DummyHead->next = head;//这里哑节点要接上
        auto p = head;//p用于计数
        int length = 0;
        while(p){
            length++;
            p = p->next;
        }//这一段用来算链表长度length
        for(int size=1; size < length; size <<= 1){
            //第一次切成每份一个数，第二次两个数。。。用size左移一位表示size*2
            auto cur = DummyHead->next;//cur表示该切的链表头部
            auto tail = DummyHead;//tail表示切完的前一个链表的尾部，用于接上下一个合并的链表
            while(cur){
                auto left = cur;//设定需要切的链表第一条链表头
                auto right = cut(left,size);//设定需要切的第二条链表表头
                cur = cut(right,size);//将cur移动到第二条链表后面

                tail->next = merge(left,right);
                while(tail->next){//注意是判断next是否存在，否则tail会指向nullptr
                    tail = tail->next;
                }
            }
        }
        return DummyHead->next;//返回哑节点后面的值
    }
    ListNode* cut(ListNode* head, int n){//n是到第几位切断,注意只切断前半段，后半段不用切断
        auto first = head;//设置标记断点前半的指针
        while(--n && first) first = first->next;//将first指针移动到断点前
        if(!first) return nullptr;//若前半段已经遍历完该链表，则返回空指针
        auto second = first->next;
        first->next = nullptr;//断开两条链
        return second;//返回后半段的链表头
    }

    ListNode* merge(ListNode* l1, ListNode* l2){//双路归并
        auto DummyHead = new ListNode(-1);//哑节点
        auto cur = DummyHead;//注意这里哑节点先不加入链表，用于创建新链表
        while(l1 && l2){
            if(l1->val < l2->val){
                cur->next = l1;
                l1 = l1->next;
            }
            else{
                cur->next = l2;
                l2 = l2->next;
            }//哪个小接哪个
            cur = cur->next;//cur指针后移一位
        }
        cur->next = l1? l1:l2;//一条链遍历完成另一条可能还有剩余，因此判断哪条有剩并接上
        return DummyHead->next;
    }
};

7. 快速排序（Quick Sort）

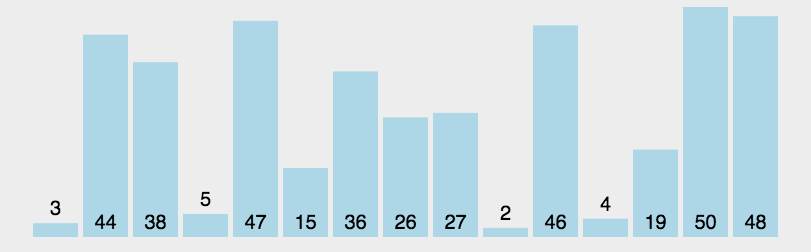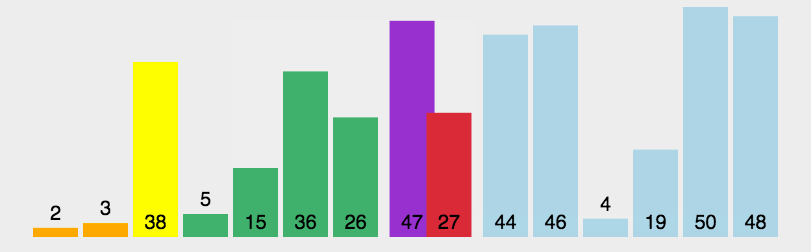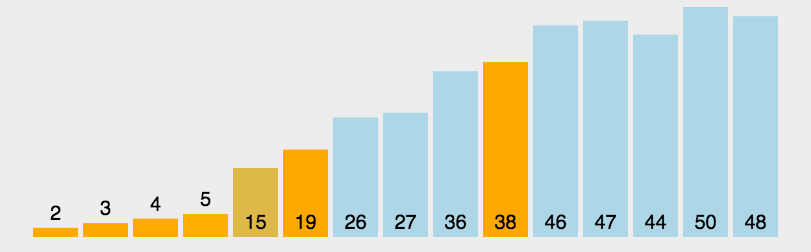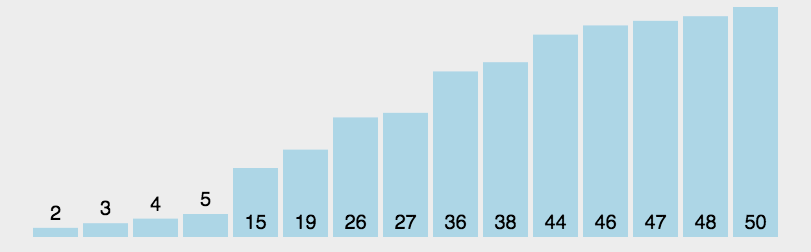
• 平均时间复杂度$O(Nlog{N})$
• 空间复杂度$O(Nlog{N})$
• 不稳定

数组
递归

#include <bits/stdc++.h>
using namespace std;
////注意：数组不能为空
///nowcoder pass
//array
int Partition(vector<int>& a, int low, int high){
    int key_value = a[low];
    while(low<high){
        while(low < high && a[high] >= key_value) high--;
        a[low] = a[high];
        while(low < high && a[low] <= key_value) low++;
        a[high] = a[low];
    }
    a[low] = key_value;
    return low;
}

void QuickSort(vector<int>& a, int start, int end){
    int mid;
    if(start<end){
        mid = Partition(a, start, end);
        QuickSort(a, start, mid-1);
        QuickSort(a, mid+1, end);
    }
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int tmp = 0;
    vector<int> a;
    int n = 0;
    cin>>n;//这个是nowcoder会用到的一个n，用来记录数组长度
    cin>>tmp;
    a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
    while(true){
        if(cin.get()=='\n') break;
        cin>>tmp;
        a.push_back(tmp);
    }

    n = a.size();
    QuickSort(a, 0, n-1);


    for(const int &e:a){
        cout<<e<<' ';
    }
    cout<<'\n';
}

链表
交换val值

交换节点

占坑

---

以下三种排序都是用空间换时间

8. 计数排序（Counting Sort）

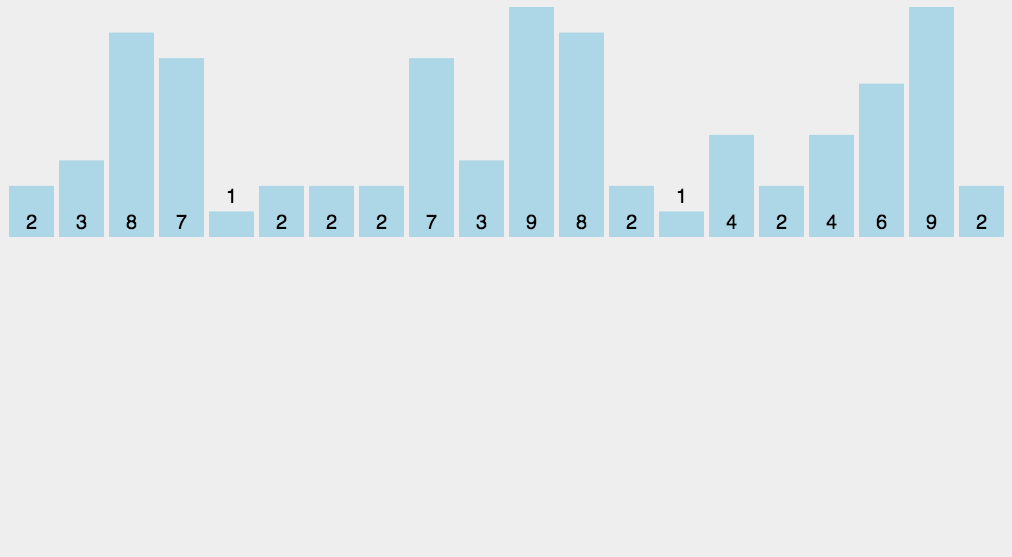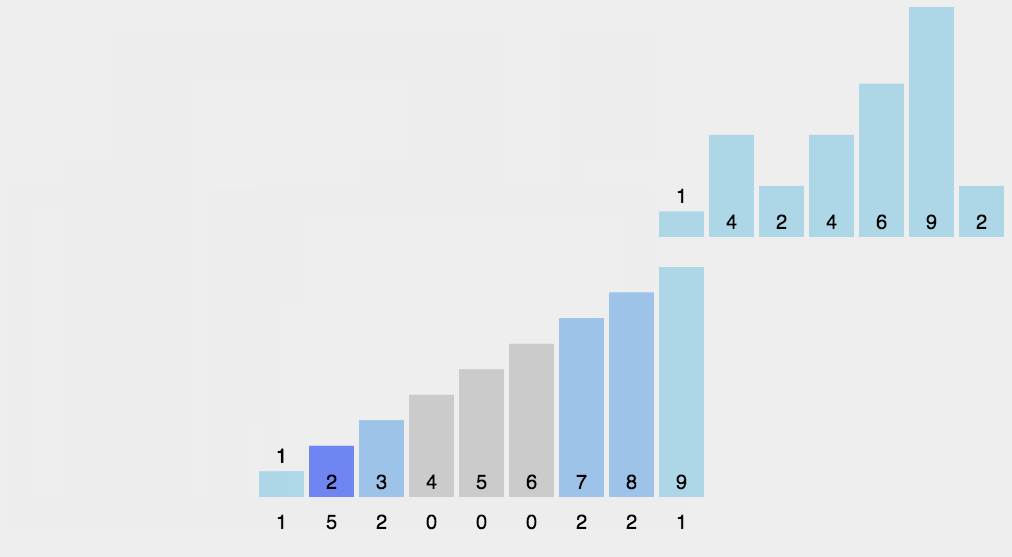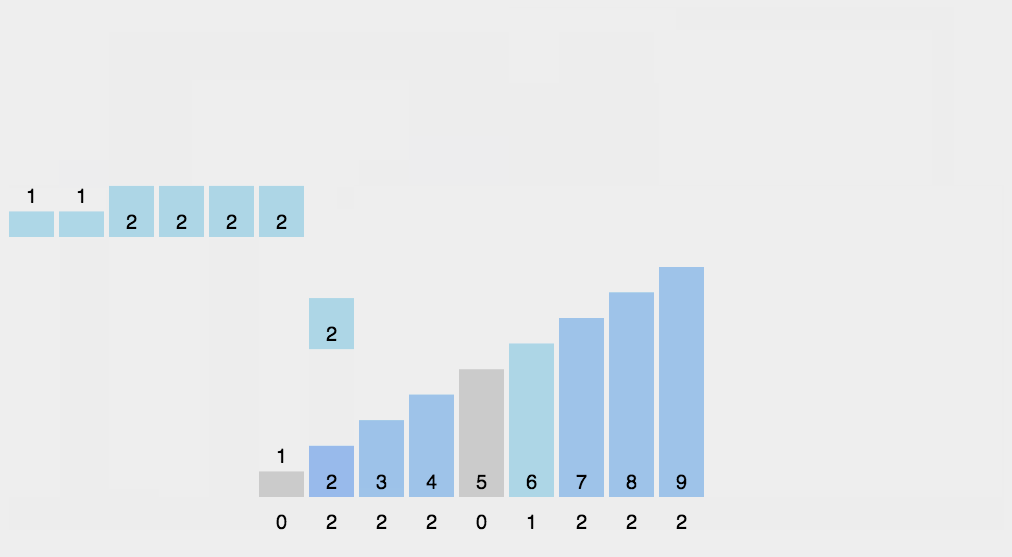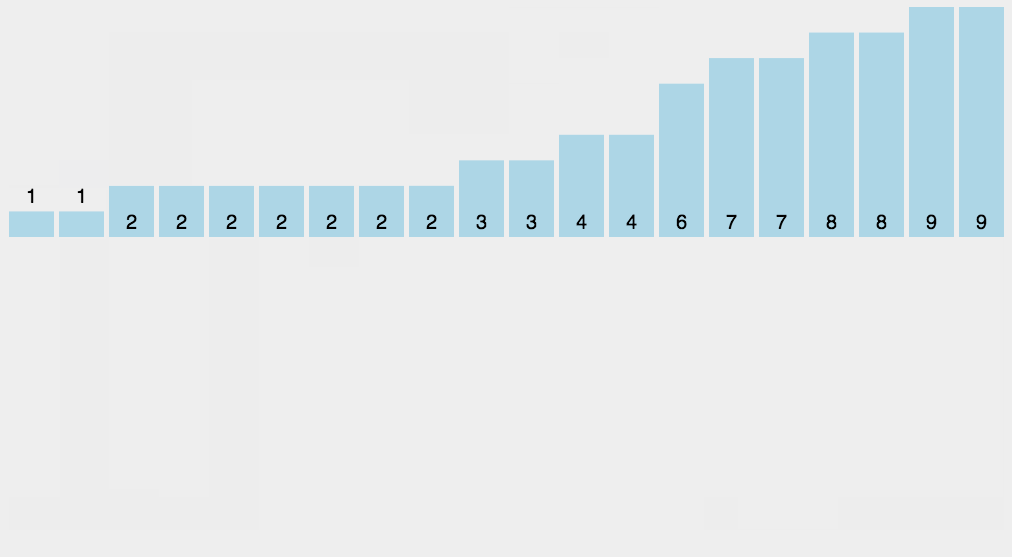
• 平均时间复杂度$O(N+K)$,K是数组最大最小值的差
• 空间复杂度$O(N+K)$
• 稳定

前面想能不能用map来计数以减少内存开销，但是若用unordered_map无法保证计数的下标递增；使用map自动排序涉及其他的时间复杂度。桶排序类似。

#include <bits/stdc++.h>
using namespace std;
////注意：数组不能为空
///nowcoder no pass,内存超了
//array
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int tmp = 0;
    vector<int> a;
    int n = 0;
    cin>>n;//这个是nowcoder会用到的一个n，用来记录数组长度
    cin>>tmp;
    a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
    while(true){
        if(cin.get()=='\n') break;
        cin>>tmp;
        a.push_back(tmp);
    }

    n = a.size();
    int max_value = INT_MIN;
    int min_value = INT_MAX;
    for(auto &v:a){
        max_value = max(v, max_value);
        min_value = min(v, min_value);
    }//遍历数组找最大值
    int b[max_value-min_value+1];
    for(auto &v:a){
        b[v-min_value]++;
    }
    a.clear();//清除原数组
    for(int i=min_value; i<max_value; i++){
        while(b[i]--){
            a.push_back(i);
        }//计数完成的数字挨个放入原数组
    }


    for(const int &e:a){
        cout<<e<<' ';
    }
    cout<<'\n';
}

9. 桶排序（Bucket Sort）

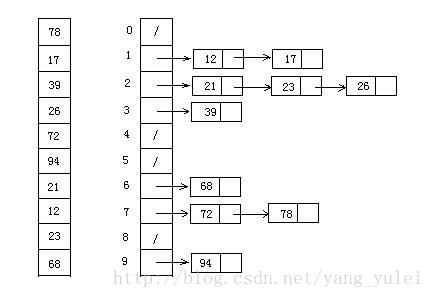
• 平均时间复杂度$O(N+K)$,K是数组最大最小值的差
• 空间复杂度$O(N+K)$
• 稳定

计数排序可以算作特殊的桶排序，即一个数一个桶
时间复杂度还得考虑每个桶的插入排序，以上的时间复杂度统计似乎未考虑
数组

#include <bits/stdc++.h>
using namespace std;
////注意：数组不能为空
///nowcoder pass
//array
//计数排序是特殊的桶排序，即每个桶只存相同的数字
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int tmp = 0;
    vector<int> a;
    int n = 0;
    cin>>n;//这个是nowcoder会用到的一个n，用来记录数组长度
    cin>>tmp;
    a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
    while(true){
        if(cin.get()=='\n') break;
        cin>>tmp;
        a.push_back(tmp);
    }

    n = a.size();
    int max_value = INT_MIN;
    int min_value = INT_MAX;
    for(auto &v:a){
        max_value = max(v, max_value);
        min_value = min(v, min_value);
    }//遍历数组找最大值
    int bucket_num = 5;//设计桶的的数量，可更改
    float bucket_range = ((float)max_value-(float)min_value+1)/5;//每个桶包含的范围，也可以用其他映射方式，注意是float
    vector<vector<int>> buckets(bucket_num);//定义二维数组保存每个桶及桶里的元素
    int bucket_key = 0;//定义记录这个数所在桶的变量
    for(auto &v:a){
        bucket_key = floor(((float)v-(float)min_value)/bucket_range);//每个数计算其所在桶
        //下面是在每个桶内执行插入排序
        if(buckets[bucket_key].empty() || v >= buckets[bucket_key].back()) buckets[bucket_key].push_back(v);
        else{
            for(int i=0; i<buckets[bucket_key].size(); ++i) {
                if (v < buckets[bucket_key][i]) {
                    buckets[bucket_key].insert(buckets[bucket_key].begin()+i, v);
                    break;
                }
            }
        }
    }
    a.clear();//原数组清空
    for(int i=0; i<bucket_num; i++){
        int thisBucketNum = buckets[i].size();
        for(int j=0; j<thisBucketNum; j++){
            a.push_back(buckets[i][j]);
        }
    }//从桶中挨个取出数组


    for(const int &e:a){
        cout<<e<<' ';
    }
    cout<<'\n';
}

链表

桶排序更适合用链表实现，定义一个vector保存表头，然后后续用链表保存，这个即可以用于链表排序也可以用于数组排序，前者是直接断链存到哦vector，后者是取数创建新的链表存入vector

占坑

10. 基数排序（Radix Sort）

• 平均时间复杂度$O(N*d)$,d为基数的个数
• 空间复杂度$O(N+d)$
• 稳定 数组

#include <bits/stdc++.h>
using namespace std;
////注意：数组不能为空
///nowcoder no pass,内存超了
//array
void countSort(vector<int>& a, int digit){
    vector<vector<int>> b(10);//定义二维数组保存数，第一维是10位
    for(auto &v:a){//遍历a中的每个数
        int this_digit = v%(digit*10)/digit;//求这个数在当前位的值
        if(b[this_digit].empty() || v >= b[this_digit].back())
            b[this_digit].push_back(v);//若这一位的数组是空的，或者比最后一个数大，直接插在最后一位
        else{
            for(int i=0; i<b[this_digit].size(); i++){
                if(v < b[this_digit][i]){
                    b[this_digit].insert(b[this_digit].begin()+i, v);
                    break;
                }
            }
        }//否则进行插入排序
    }

    a.clear();//清空原数组
    for(int i=0; i<b.size(); i++){
        for(int j=0; j<b[i].size(); j++){
            a.push_back(b[i][j]);
        }
    }//挨个取数存入原数组
    b.clear();
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int tmp = 0;
    vector<int> a;
    int n = 0;
    cin>>n;//这个是nowcoder会用到的一个n，用来记录数组长度
    cin>>tmp;
    a.push_back(tmp);//注意用cin.get()要先输入一个数字，然后用cin.get()去接受空格和回车
    while(true){
        if(cin.get()=='\n') break;
        cin>>tmp;
        a.push_back(tmp);
    }

    n = a.size();
    int max_value = INT_MIN;
    for(auto &v:a){
        max_value = max(v, max_value);
    }//遍历数组找最大值
    int mag = 1;//定义最大数的数量级
    while(max_value/mag > 10) mag *= 10;

    for(int i=1; i<=mag; i *= 10){
        countSort(a, i);//调用按位的计数排序
    }




    for(const int &e:a){
        cout<<e<<' ';
    }
    cout<<'\n';
}

参考

参考自

1. https://www.cnblogs.com/tenosdoit/p/3666585.html
2. https://www.cnblogs.com/onepixel/articles/7674659.html
3. https://blog.csdn.net/Koala_Tree/article/details/79958965
4. https://zhuanlan.zhihu.com/p/57088609 第四个我还没具体看，网址先放在这里
5. https://www.runoob.com/w3cnote/ten-sorting-algorithm.html
6. https://www.runoob.com/w3cnote/sort-algorithm-summary.html