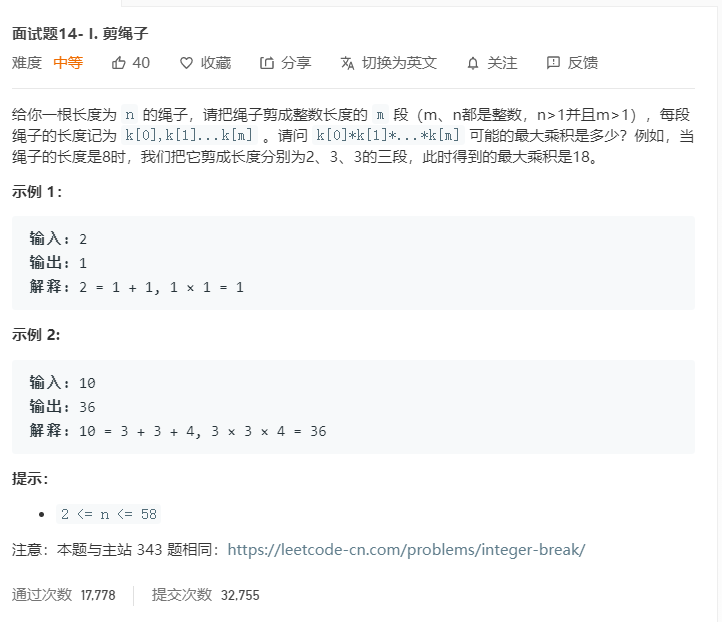
题目

题解

1. 普通DP

具体思路看注释。前面遇到一个问题，即循环里dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]));为什么不是dp[i], j*(i-j), dp[j]*dp[i-j]
这是因为在内循环时，随着j的增大，就包括了dp[j]中的分割情况，因此不用dp[j]来计算。即有可能dp[j]大于j，但是在前面j的分割值中已经计算过了。
但是对于dp[i-j]如果也这么思考就不对了，若把dp[i-j]改成i-j就会缺失很多种分割情况，即j，i-j至少有一个需要用dp以包含多种分割情况。
经过测试，写成

dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]));
dp[i] = max(dp[i], max(j*(i-j), dp[j]*(i-j)));

都是对的。但是写成

dp[i] = max(dp[i], max(j*(i-j), dp[j]*dp[i-j]));

会报错。这是因为dp[i]至少要分割一次，不包含不分割自身的情况。

  • 时间复杂度$O(n^{2})$，双循环
  • 空间复杂度$O(n)$，dp数组
class Solution {
public:
    int cuttingRope(int n) {
        vector<int> dp(n+1);
        //由题目可知，n不为0和1，且dp[0]和dp[1]是没用的，因为在求切分的最大值时j*(i-j)中的j=1时已经承担了dp[1]的作用，而0是完全用不到，因此初始化dp[2]即可
        dp[2] = 1;
        //外循环从下往上生成dp数组，绳子越来越长
        for(int i=3; i<=n; ++i){
            //内循环遍历所有切割点，前半段绳子从1开始到n-1
            for(int j=2; j<i; ++j){
                //dp[i]是暂存本次内循环中的最大乘积
                //j*(i-j)是切断后两边直接相乘的结果
                //j*dp[i-j]是切断后后半段继续切，后半段获得乘积最大值
                dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]));
            }
        }
        return dp[n];
    }
};

2. 贪婪算法

看Krahets大神的分析可知，每一段取3时最终的乘积最大，即要使绳子每一段的3尽量多一点。那么就可以计算$a=n/3$，然后计算3的a次幕。需要注意的是对余数b的处理，有三种情况：

  1. b==0。直接返回pow(3,a)
  2. b==1。需要拆一个前面的3，将3和1变为2和2。因为3×1>2×2
  3. b==2。直接返回pow(3,a)*2
  • 时间复杂度$O(1)$
  • 空间复杂度$O(1)$
class Solution {//两种方法。2.贪婪
public:
    int integerBreak(int n) {
        if(n<4) return n-1;//n为2，3时，返回1，2。n不能为0，1
        int a = n/3, b = n%3;//计算n除以3的商和余数
        if(b==0) return pow(3,a);
        else if(b==1) return pow(3,a-1)*4;
        else return pow(3,a)*2;
    }
};