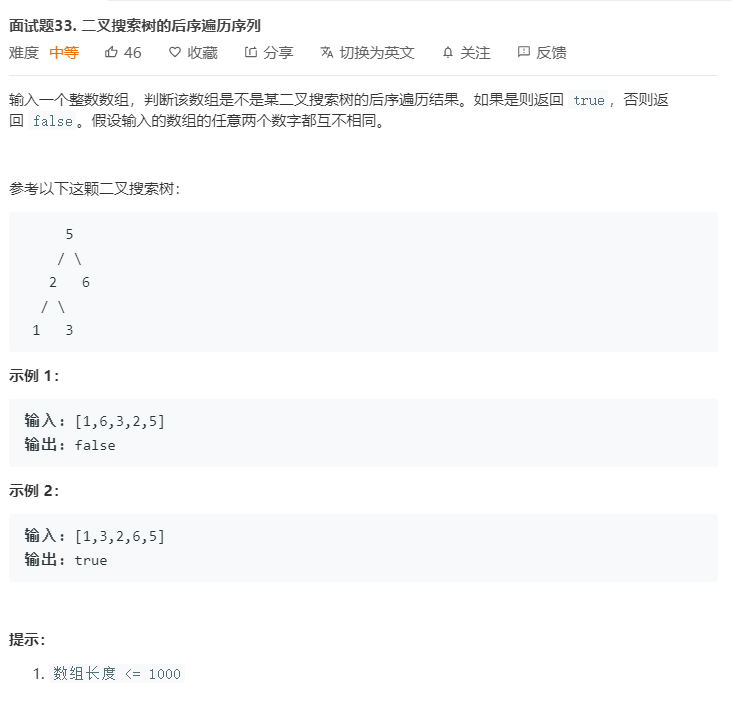
题目

题解

二叉树结构如下：

//Definition for a binary tree node.
    struct TreeNode {
        int val;
        TreeNode *left;
        TreeNode *right;
        TreeNode(int x) : val(x), left(NULL), right(NULL) {}
    };

1. 分治递归法

二叉搜索树的性质见这里。后序遍历的顺序是左->根->右。因此二叉搜索树的后序遍历数组有如下性质：

  1. 最后一个数是搜索树的根节点
  2. 数组中left~mid-1的数均小于根节点
  3. 数组中mid~eight-1的数均大于根节点
  4. 递归左右子树也满足上述条件
  • 时间复杂度最好$O(n)$；最差$O(n^{2})$
  • 空间复杂度$O(n)$
class Solution {//两种方法。1.分治递归
public:
    bool help(vector<int>& postorder, int left, int right){
        if(left>=right) return true;//只剩一个节点，返回true
        int i = left;//设置指针i从left开始
        while(postorder[i]<postorder[right]) i++;//跳过所有小于最后一位根节点的数，找到左右子树的分界
        int mid = i;//找到右子树的起始位置
        while(postorder[i]>postorder[right]) i++;//跳过所有大于根节点的数字，找到根节点
        //判断是否为二叉搜索树
        //1.此时i应当指向right，即mid~right直接都是右子树的节点
        //2.递归进入左子树进行判断
        //3.递归进入右子树进行判断
        return i==right && help(postorder,left,mid-1) && help(postorder,mid,right-1);
    }
    bool verifyPostorder(vector<int>& postorder) {
        return help(postorder, 0, postorder.size()-1);
    }
};

2. 辅助单调栈

先倒序数组，即后序遍历的翻转数组，遍历顺序未根，右，左。定义一个root为INT_MAX，再定义一个单调递增栈。具体细节见注释。

  • 时间复杂度$O(n)$
  • 空间复杂度$O(n)$
class Solution {//两个方法。2.辅助单调栈
public:
    bool verifyPostorder(vector<int>& postorder) {
        stack<int> s;
        int tmp_root = INT_MAX;//先让tmp_root等于最大，相当于把整个二叉树当成INT_MAX的左子树，进行迭代判断
        for(int i=postorder.size()-1; i>=0; --i){//从后向前，即根->右->左的顺序进行迭代
            if(postorder[i]>=tmp_root) return false;//若左子树有一个数大于根，报错
            //当s不为空，且下一个数小于小于当前栈顶时，说明进入新的左子树了，此时要更换tmp_root
            //新tmp_root是大于该节点的数中最小的一个
            //所有大于该节点的数均出栈
            while(!s.empty() && s.top()>postorder[i]){
                tmp_root = s.top();s.pop();
            }
            //其他情况就不停的入栈，相当于一直进入右子树
            s.push(postorder[i]);
        }
        //全部遍历完成未出错返回ture
        return true;
    }
};