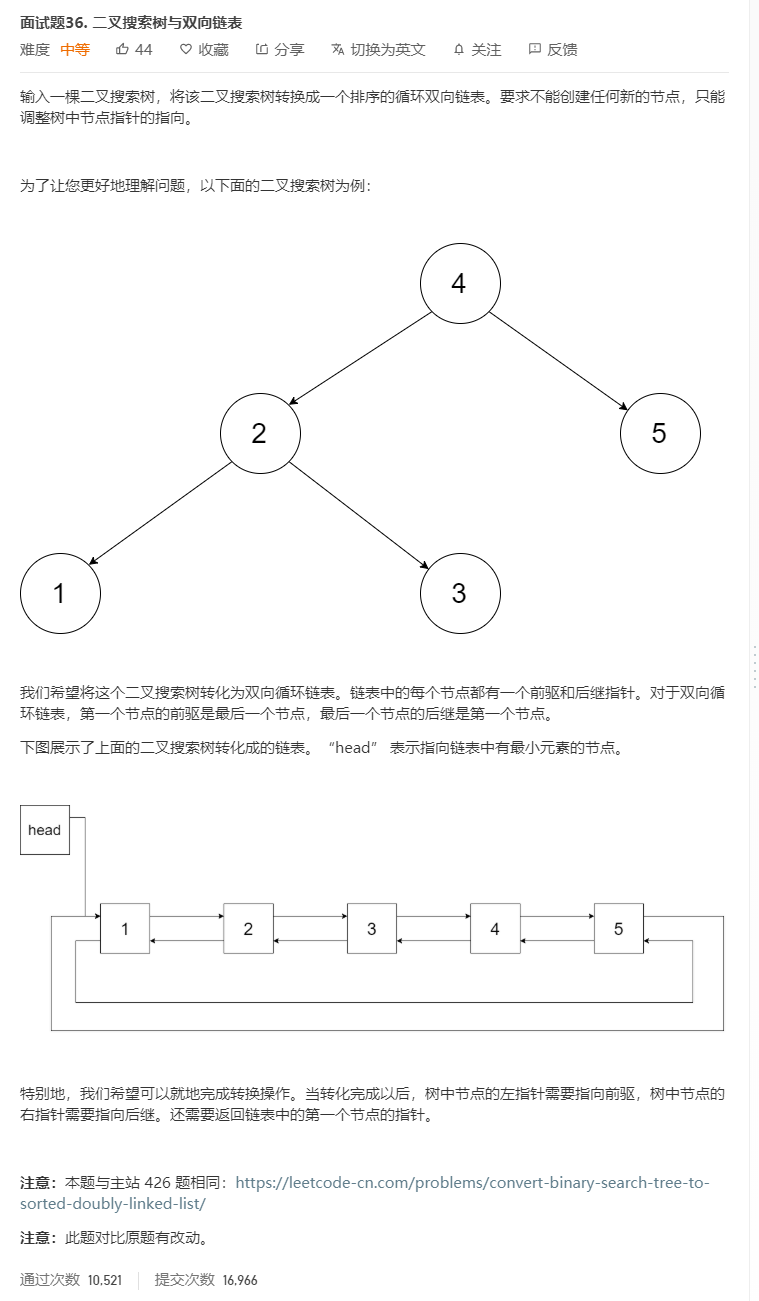
题目

题解

节点定义如下：

// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};

这道题要利用二叉搜索树的性质，即二叉搜索树的中序遍历是有序数组，二叉搜索树的详细性质见这里。二叉查找树性质如下：

二叉查找树（BST：Binary Search Tree）是一种特殊的二叉树，它改善了二叉树节点查找的效率。二叉查找树有以下性质： 对于任意一个节点 n，

  • 其左子树（left subtree）下的每个后代节点（descendant node）的值都小于节点 n 的值；
  • 其右子树（right subtree）下的每个后代节点的值都大于节点 n 的值。

因此这道题的思路是用递归的放松中序遍历二叉搜索树，并在遍历中调整每一个节点的左右指针

class Solution {//使用递归进行中序遍历重建二叉树为链表
    Node *pre, *head;//定义两个全局指针，用来在递归中存中序遍历的上一个节点和头节点
public:
    //定义递归函数
    void dfs(Node* cur){
        if(!cur) return;//遇到空节点直接返回，说明越过叶节点
        //以下是中序遍历，左中右
        dfs(cur->left);//递归左子树
        //处理中间节点
        if(!pre) head = cur;//当pre为空时，说明当前是中序遍历的第一个节点，head指向当前节点
        else pre->right = cur;//pre不为空，则将pre的右指针指向当前节点
        cur->left = pre;//cur的左指针指向怕热，形成双向链表
        pre = cur;//移动pre到cur
        dfs(cur->right);//递归右子树
    }
    Node* treeToDoublyList(Node* root) {
        if(!root) return root;
        dfs(root);//递归根节点
        //下面两部是将已经建立好的双向链表首尾连接
        pre->right = head;
        head->left = pre;
        return head;
    }
};