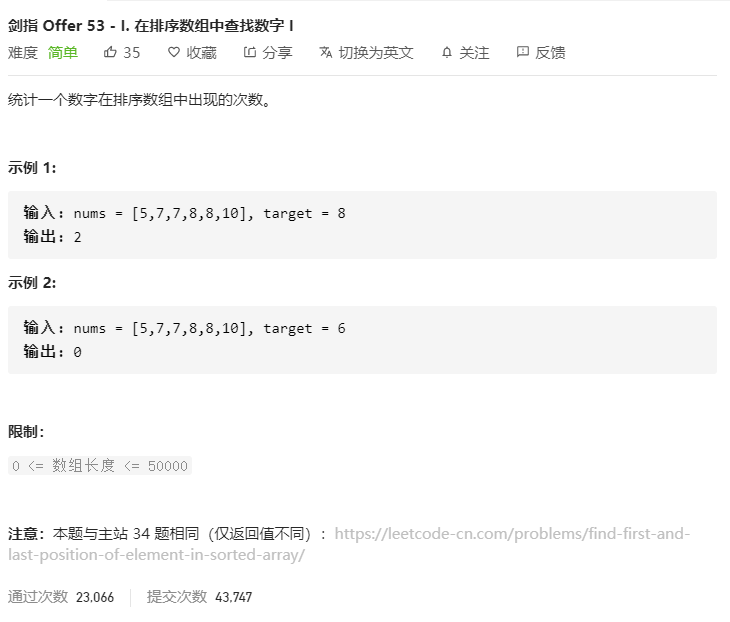
题目

题解

1. 挨个查找法

  • 时间复杂度$O(N)$
  • 空间复杂度$O(1)$

就是挨个查找数组，找到的第一个就是开始位置，找到的最后一个就是结束位置。
这个比较好写，但是对于这道题会超时

2. 二分查找法

  • 时间复杂度$O(logN)$
  • 空间复杂度$O(1)$

利用二分查找的性质，可以缩短时间复杂度

class Solution {
public:
    int search(vector<int>& nums, int target) {
        if(nums.empty()) return 0;
        //起始位置
        int start = find1stNum(nums, target);
        //起始位置判断不合规直接返回0
        if(start > nums.size() - 1 || nums[start] != target) return 0;
        //结束位置，是找比target大1的数的位置-1，由于最后计算位置差的时候还要+1
        //因此这里把结束位置标记为最后一个target的下一个位置
        int end = find1stNum(nums, target + 1) ;
        //计算位置差
        return end - start;
    }

    //二分查找找起始位置
    int find1stNum(vector<int>& nums, int target){
        //注意right不用-1，因为寻找end的时候是找到其下一个的位置
        int left = 0, right = nums.size();
        //二分查找
        while(left<right){
            int mid = left + (right - left) / 2;
            //注意这里用 < 才能找到第一个为target的位置
            if(nums[mid] < target) left = mid + 1;
            else right = mid;
        }
        return left;
    }
};