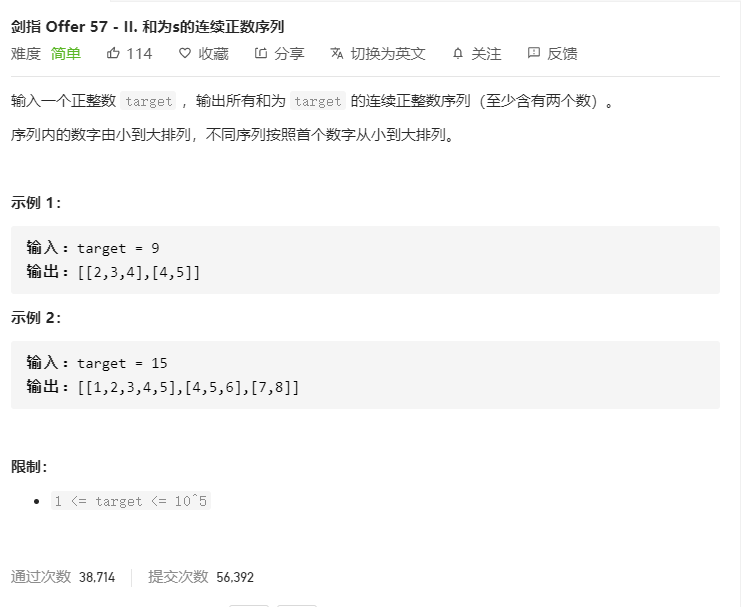
题目

题解

1. 暴力法

挨个计算所有数组的和，时间复杂度太高

  • 时间复杂度: $O(n^{2})$
  • 空间复杂度: $O(1)$

2. 滑动窗口法

看注释吧，不太难，证明可以看题解

  • 时间复杂度: $O(n)$
  • 空间复杂度: $O(1)$
class Solution {//三个方法。1.滑动窗口
public:
    vector<vector<int>> findContinuousSequence(int target) {
        //左闭右开区间，起初sum为0
        int left = 1, right = 1;
        int sum = 0;
        vector<vector<int>> res;
        //！！注意这个终止条件
        while(right <= target / 2 + 2){
            //sum小于target右边界右移
            if(sum < target){
                sum += right;
                right++;
            //sum大于target左边界右移
            }else if(sum > target){
                sum -= left;
                left++;
            //sum等于target存结果，并左边界左移
            }else{
                vector<int> arr;
                for(int i = left; i < right; ++i) arr.push_back(i);
                res.push_back(arr);
                sum -= left;
                left++;
            }
        }
        return res;
    }
};

3. 等差数列通项公式法

来自erick_chen。这个方法很牛逼，理解起来更容易一点

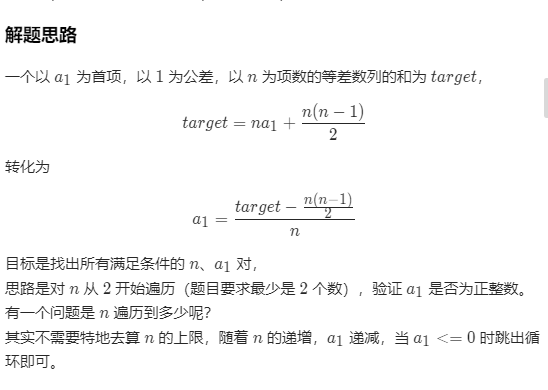
注意几个点：

  1. n从2开始，因为题目要求数组至少有两个数
  2. 借鉴题解2，其实n到不了target+1，在分子小于0的时候循环就停止了
  3. 随着n增加，tmp和a1都递减
  4. 只有tmp/n为正整数的时候，该结果才有效
  5. 注意res要从前面插入结果，否则其数列顺序和结果是相反的
  • 时间复杂度: $O(n)$
  • 空间复杂度: $O(1)$
class Solution {//三个方法。2.等差数列通项公式法
public:
    vector<vector<int>> findContinuousSequence(int target) {
        vector<vector<int>> res;
        for(int n=2; n < target + 1; ++n){
            int tmp = target - n * (n - 1) / 2;
            if(tmp < 1) break;
            if(tmp % n == 0){
                int a1 = tmp / n;
                vector<int> arr;
                for(int i = a1; i <= a1 + n - 1; ++i) arr.push_back(i);
                res.insert(res.begin(), arr);
            }
        }
        return res;
    }
};

4. 求根公式法

和3的思路类似，也是用等差数列的思想，但是是用求根公式求解，而且会有复数情况，个人感觉理解起来比较困难

  • 时间复杂度: $O(n)$
  • 空间复杂度: $O(1)$
占坑