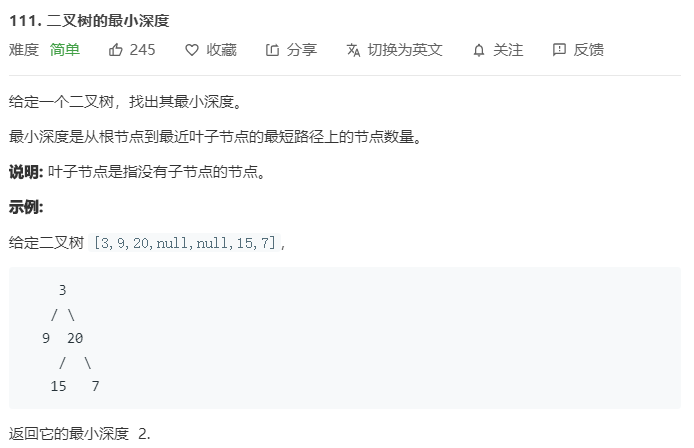
题目

题解

二叉树结构如下：

//Definition for a binary tree node.
    struct TreeNode {
        int val;
        TreeNode *left;
        TreeNode *right;
        TreeNode(int x) : val(x), left(NULL), right(NULL) {}
    };

1. 递归法

  • 时间复杂度: $O(N)$
  • 空间复杂度: 最坏情况下，整棵树是非平衡的，例如每个节点都只有一个孩子，递归会调用 $N$ （树的高度）次，因此栈的空间开销是 $O(N)$ 。但在最好情况下，树是完全平衡的，高度只有 $\log(N)$，因此在这种情况下空间复杂度只有 $O(\log (N))$ 。
class Solution {
public:
    int minDepth(TreeNode* root) {//两种方法。1、递归
        if(!root) return 0;//特殊情况
        if(!root->left) return 1+minDepth(root->right);
        if(!root->right) return 1+minDepth(root->left);//这两行是和#104的主要区别，不存在左右子树时不算其深度。注意这里也要+1
        return min(minDepth(root->left),minDepth(root->right))+1;//这个和#104一样，递归，用+1来计算每一层层数
    }
};

2. 队列迭代法

  • 时间复杂度: 最坏情况下，这是一棵平衡树，我们需要按照树的层次一层一层的访问完所有节点，除去最后一层的节点。这样访问了 $N/2$ 个节点，因此复杂度是 $O(N)$。
  • 空间复杂度: 最和时间复杂度相同，也是 $O(N)$
class Solution {
public:
    int minDepth(TreeNode* root) {//两种方法。2、队列迭代法
        int level = 0;
        if(!root) return level;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty()){
            level++;//和#104的区别，遍历一层之前计数
            for(int i=q.size();i>0;i--){
                TreeNode *cur = q.front();q.pop();
                if(!cur->right && !cur->left) return level;//和#104的区别，当两个子树都为空时返回层数
                if(cur->left) q.push(cur->left);
                if(cur->right) q.push(cur->right);
            }
        }
        return -1;//运行到这里说明出错了
    }
};