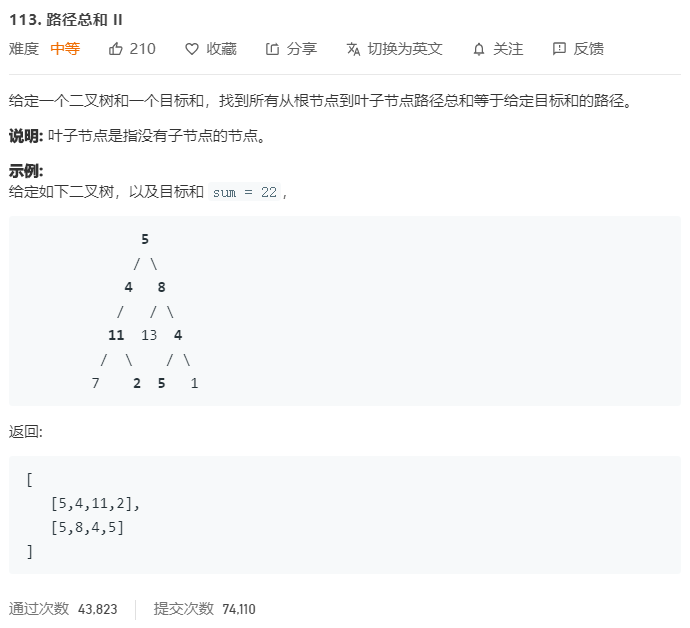
题目

题解

二叉树结构如下：

//Definition for a binary tree node.
    struct TreeNode {
        int val;
        TreeNode *left;
        TreeNode *right;
        TreeNode(int x) : val(x), left(NULL), right(NULL) {}
    };

1. 递归法

  • 时间复杂度：$O(N)$
  • 空间复杂度：$O(N)$ 需要额外空间。
class Solution {//两个方法。1.递归
public:
    vector<vector<int>> pathSum(TreeNode* root, int sum) {
        vector<vector<int>> res;//定义保存最终结果的二维数组
        vector<int> oneRes;//定义保存本次结果的一维数组
        helper(root,sum,res,oneRes);//递归
        return res;
    }

    void helper(TreeNode* node, int sum, vector<vector<int>> &res, vector<int> &oneRes){
        if(!node) return;//该节点为空时直接返回
        oneRes.push_back(node->val);//先把该节点的值压入栈
        if(!node->left && !node->right && node->val == sum){
            res.push_back(oneRes);
        }//当该节点为叶节点，且该路径和已经为sum时，把oneRes压入res
        helper(node->left, sum-node->val, res, oneRes);
        helper(node->right, sum-node->val, res, oneRes);//对左右子树进行递归
        oneRes.pop_back();//若递归出栈，则将oneRes压入的值取出，存储新的路径
    }
};

2. 栈迭代法

这个方法借鉴后序遍历，具体见二叉树的三种遍历中的后序遍历部分。

  • 时间复杂度：$O(N)$
  • 空间复杂度：$O(N)$ 需要额外空间。
 //#112的升级版，要记录该路径上的值，注意题干是保存每一条路径，所以要全部遍历
class Solution {//两个方法。2.栈迭代，类似后序遍历
public:
    vector<vector<int>> pathSum(TreeNode* root, int sum) {
        vector<vector<int>> res;
        if(!root) return res;
        vector<TreeNode*> st;//用一位数组，因为中间要取数出来
        TreeNode *cur = root;//用cur指向根节点
        TreeNode *last = nullptr;//last用于存储上一次指遍历输出的值，先设置为nullptr
        int oneSum = 0;//oneSum用于存储当前路径的和
        while(cur || !st.empty()){//只有cur指向nullptr且栈s空了才停止遍历。cur指向nullptr可能是遍历完一个子树；s空了可能回到根节点。
            if(cur){
                st.push_back(cur);
                oneSum += cur->val;
                cur = cur->left;
            }//先不断进入左子树，并存储当前路径上的值
            else{//若左子树遍历完成进入到最后的节点
                TreeNode *tmp = st.back();//暂存栈顶的值
                if(!tmp->left && !tmp->right && oneSum == sum){//若该节点是叶节点且路径的和等于sum
                    vector<int> oneRes;
                    for(auto &s: st) oneRes.push_back(s->val);
                    res.push_back(oneRes);
                }//设置一维数组存储这条路径上的值，栈（这里用vector）存储的就是这条路径上的每个节点。
                if(tmp->right && tmp->right != last){
                //如果栈顶的节点存在右子树，且右子树没去过
                    cur = tmp->right;//进入右子树
                }
                else{//如果没有右子树，或者右子树去过了，弹出栈顶，减去oneSum中该节点的值，并在last中存储该节点
                    st.pop_back();
                    oneSum -= tmp->val;
                    last = tmp;
                }
            }
        }
        return res;
    }
};