题目

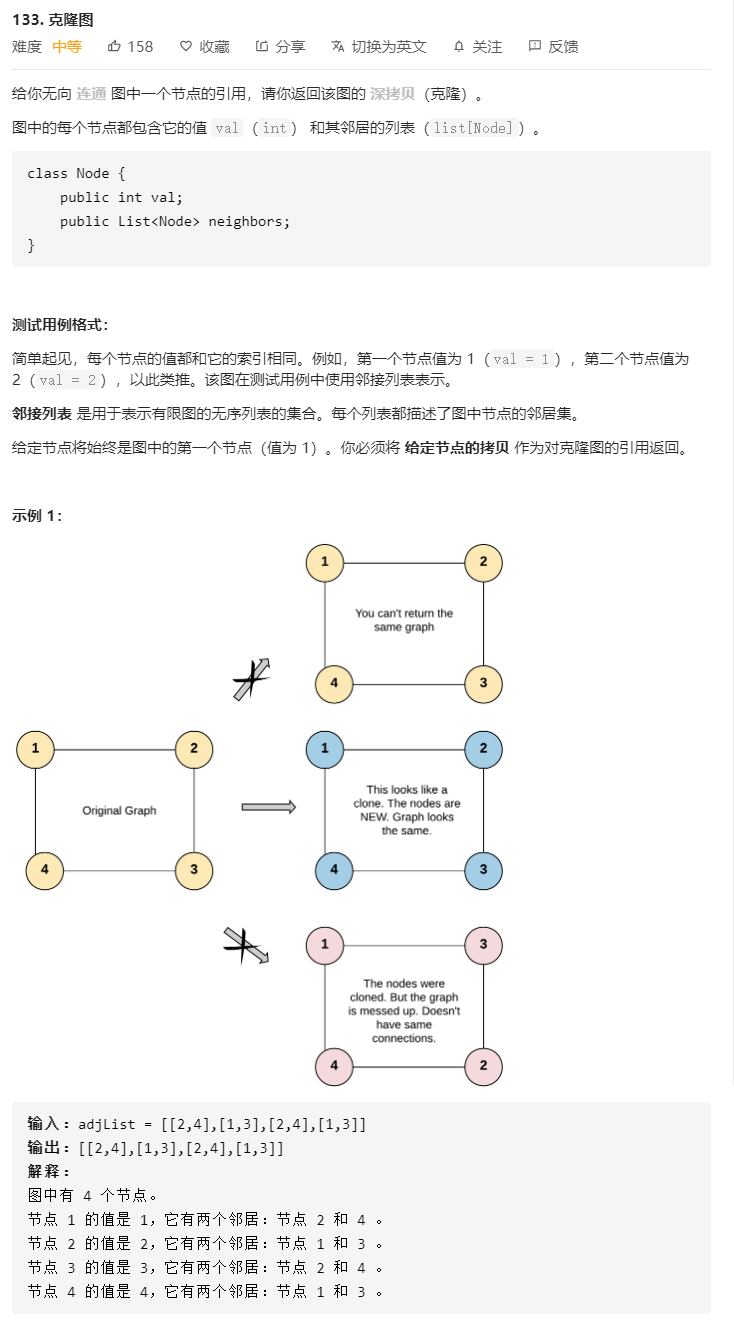
图的定义如下：

// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;
    
    Node() {
        val = 0;
        neighbors = vector<Node*>();
    }
    
    Node(int _val) {
        val = _val;
        neighbors = vector<Node*>();
    }
    
    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};

题解

两个方法。DFS，BFS

1. DFS

  • 时间复杂度$O(N)$
  • 空间复杂度$O(N)$

用一个unorder_map联系新旧两个图。从当前节点开始挨个复制，如果当前节点已经复制过则直接从map里面取

class Solution {//两个方法。1.DFS
    //hash_map用于联系新旧两个图
    unordered_map<Node*, Node*> old_new;
public:
    Node* cloneGraph(Node* node) {
        return dfs(node);
    }

    Node* dfs(Node* a){
        if(!a) return nullptr;
        if(old_new.count(a)) return old_new[a];
        auto b = new Node(a->val);//复制当前节点
        old_new[a] = b;//将该节点的新旧节点均复制到map中
        //挨个dfs当前节点的每一个邻居节点
        for(auto n : a->neighbors){
            b->neighbors.emplace_back(dfs(n));
        }
        return b;
    }
};

2. BFS

  • 时间复杂度$O(N)$
  • 空间复杂度$O(N)$

和DFS类似，只是多了一个队列q用于遍历当前节点的所有邻节点

class Solution {//两个方法。2. BFS
public:
    Node* cloneGraph(Node* node) {
        if(!node) return nullptr;
        unordered_map<Node*, Node*> old_new;//定义关联新旧图各节点的map
        auto new_node = new Node(node->val);//先复制第一个节点
        old_new[node] = new_node;//关联第一个节点
        queue<Node*> q;
        q.push(node);//定义队列并压入第一个节点，用于BFS
        while(!q.empty()){
            auto tmp = q.front(); q.pop();//先取第一个节点
            //挨个处理当前节点的每一个邻节点
            for(auto n : tmp->neighbors){
                //若这个邻节点还没有加入map，则加入，并加入队列q
                if(!old_new.count(n)){
                    old_new[n] = new Node(n->val);
                    q.push(n);
                }
                //若已经加入map。直接添加到当前处理的节点的邻节点中
                //加入map说明已经遍历过其所有的邻节点，不用加入队列q中
                //若没加入map。上一步将其加入了，再进行这一步的处理
                old_new[tmp]->neighbors.emplace_back(old_new[n]);
            }
        }
        return new_node;
    }
};