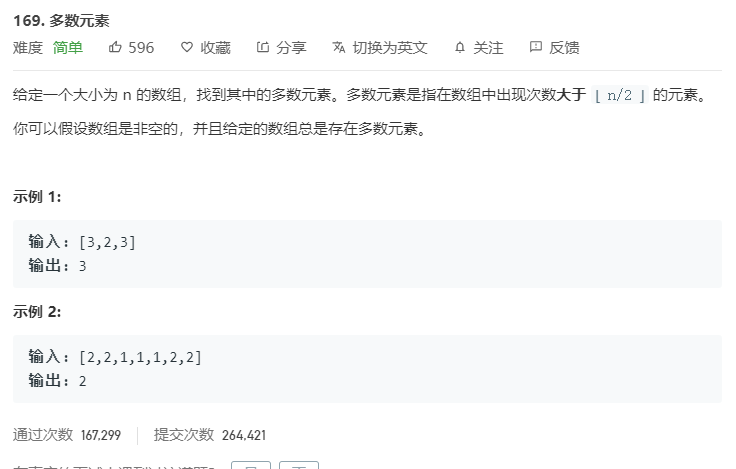
题目

题解

1. 排序取中法

  • 时间复杂度$O(nlog{n})$，主要是排序耗费的
  • 空间复杂度$O(1)$
class Solution {//三种方法，这是1.排序后取中间数
//时间复杂度O(nlogn),主要是排序消耗时间
public:
    int majorityElement(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        return nums[nums.size()/2];
    }
};

2. 摩尔投票法

最佳方法。利用本题大于n/2的性质，

  1. 先假定当前数位众数，
  2. 若遇到这个数（包括自身）则计数值+1，遇到不同的数计数值-1。
  3. 当计数值==0的时候更改当前的假定众数，为现在遍历的数
  4. 返回最后的众数值
  • 时间复杂度$O(n)$
  • 空间复杂度$O(1)$
class Solution {//三种方法，这是2.摩尔投票法，只适用于本题中众数>n/2的情况
//时间复杂度O(n),一次遍历
public:
    int majorityElement(vector<int>& nums) {
        int count = 0;//设置count计数
        int res = 0;//设置初始的res结果值
        for(int num:nums){//遍历整个数组
            if(count == 0) {
                res = num;
                count++;//如果计数到0，则更改结果值为当前遍历到的num,同时计数加1
            }
            else (res == num)? count++:count--;
            //如果计数未到0，则若num==res，计数+1，否则-1
        }
        return res;//最后遍历完成的res就是结果
    }
};

3. 哈希表法

记录每个数的个数，遇到大于一半地直接返回

  • 时间复杂度$O(n)$
  • 空间复杂度$O(n)$
class Solution {//三种方法，这是3.哈希表法，即用哈希表存储每个数出现的次数，最后取出现最多的数
//时间复杂度O(n),一次遍历
public:
    int majorityElement(vector<int>& nums) {
        unordered_map<int,int> m;//设置哈希表
        for(int num:nums){//一次遍历
            m[num]++;//统计每个数出现的次数
            if(m[num]>nums.size()/2) return num;//当这个数出现超过m/2时直接返回该值
        }
        return -1;//最好防止报错
    }
};