[Lc]107二叉树的层次遍历2

题目

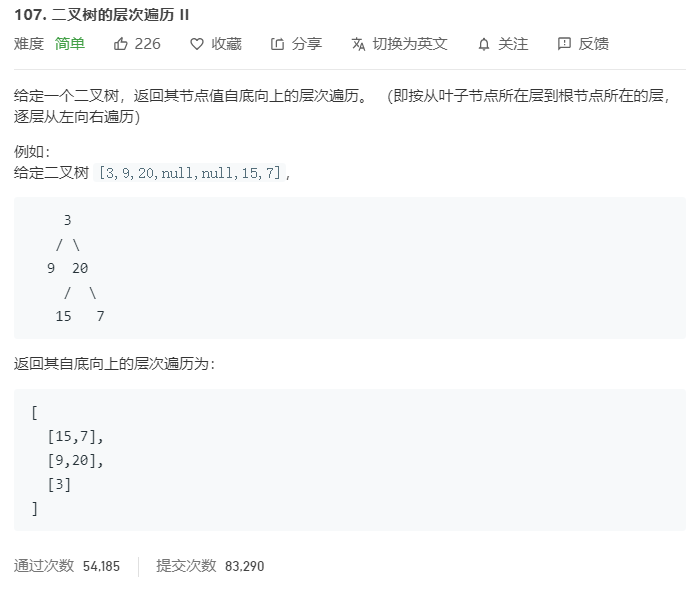
题解

二叉树结构如下：

//Definition for a binary tree node.
    struct TreeNode {
        int val;
        TreeNode *left;
        TreeNode *right;
        TreeNode(int x) : val(x), left(NULL), right(NULL) {}
    };

1. 递归法

递归法有两种思路,一种直接翻转最终数组,一种在插入时就改变顺序.

思路一:翻转数组

时间复杂度: $O(N)$
空间复杂度: $O(N)$

class Solution {
vector<vector<int>> res;
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        if(!root) return res;
        helper(root,0);
        return vector<vector<int>> (res.rbegin(),res.rend());//与#102的主要区别
    }

    void helper(TreeNode* cur,int level){
        if(!cur) return;
        if(res.size() <= level) res.push_back({});
        res[level].push_back(cur->val);
        helper(cur->left,level+1);
        helper(cur->right,level+1);
    }
};

思路二:插入时改变顺序

时间复杂度: $O(N)$
空间复杂度: $O(N)$

class Solution {
vector<vector<int>> res;
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        if(!root) return res;
        helper(root,0);
        return res;
    }

    void helper(TreeNode* cur,int level){
        if(!cur) return;
        vector<int> emptyArray;//与#102的区别
        if(res.size() == level) res.insert(res.begin(),emptyArray);//区别
        res[res.size()-1-level].push_back(cur->val);//区别
        helper(cur->left,level+1);
        helper(cur->right,level+1);
    }
};

2. 队列迭代法

时间复杂度: $O(N)$
空间复杂度: $O(N)$

class Solution {//两种方法1. 队列迭代法
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        vector<vector<int>> res;
        if(!root) return res;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty()){
            vector<int> thisLevel;
            for(int i=q.size(); i>0; i--){
                TreeNode *cur = q.front();q.pop();
                thisLevel.push_back(cur->val);
                if(cur->left) q.push(cur->left);
                if(cur->right) q.push(cur->right);
            }
            res.insert(res.begin(),thisLevel);//和#102的区别
        }
        return res;
    }
};