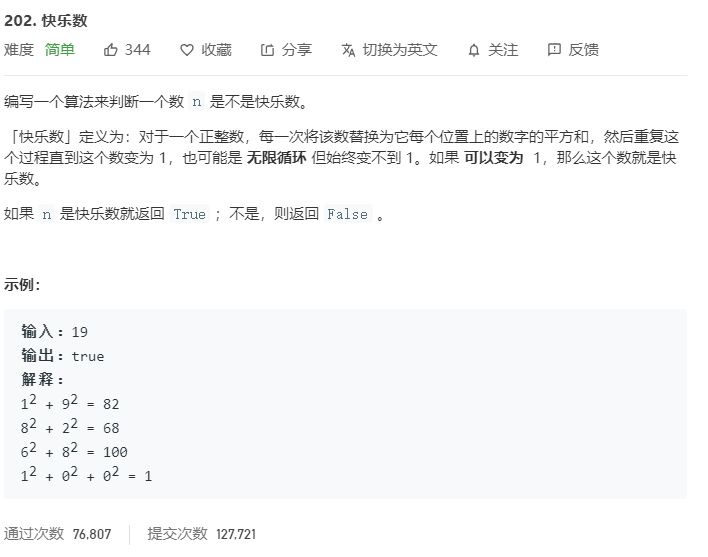
题目

题解

这题相当于142题的一个变形，相当于链表找环，但是不用找到起始点，判断是环就可以（这么说应该是141题）

1. set存值法

  • 时间复杂度$O(n)$
  • 空间复杂度$O(n)$
class Solution {
public:
    bool isHappy(int n) {//两种方法。1set存值法
        unordered_set<int> s;//定义无序set存值
        while(n!=1){//没“快乐”到1就继续
            if(s.count(n)) return false;//遇到已经遍历过的就返回false
            s.insert(n);//存入当前数
            int tmp=0;//暂存下一个数
            while(n>0){
                tmp += (n%10)*(n%10);
                n /= 10;
            }//计算出下一个数
            n = tmp;//放入n中
        }
        return true;//循环结束说明到1了，是快乐数
    }
};

2. 快慢指针法

  • 时间复杂度$O(n)$
  • 空间复杂度$O(1)$
class Solution {//两种方法。2快慢指针法
public:
    //定义获取下一个数的函数
    int getNext(int n){
        int res=0;
        while(n>0){
            res += (n%10)*(n%10);
            n /= 10;
        }//挨个每一位平方加起来
        return res;
    }
    bool isHappy(int n) {
        int p1 = n, p2 = n;
        while(true){
            if(p1 == 1 || p2 ==1) return true;//两个中间有一个到1了就可以返回true
            //快指针动两步。慢指针动一步
            cout<<p1<<' '<<p2<<'\n';
            p1 = getNext(p1);
            p2 = getNext(p2);
            p2 = getNext(p2);
            if(p1 == p2) break;//相遇跳出循环
        }
        return p1==1;//又可能两个指针各动一次就到1了，这时两指针同时等于1相等，这时就要返回true，其他情况返回false，用p1==1判断
    }
};