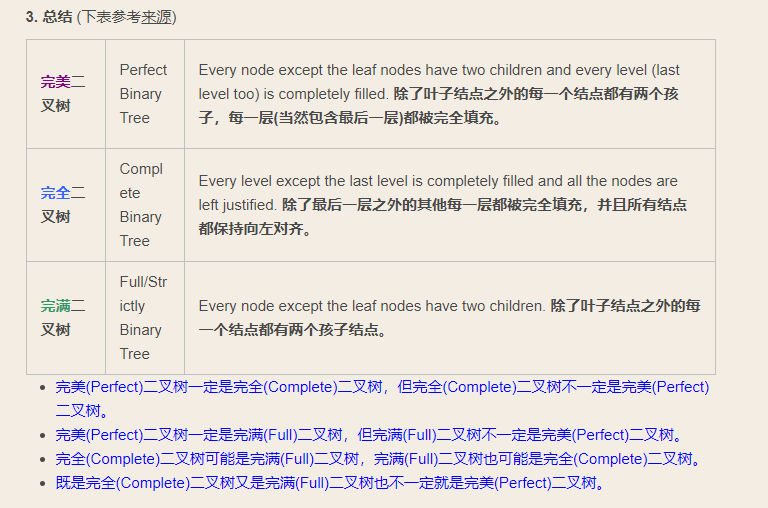
[Lc]222完全二叉树的节点个数
Contents
题目
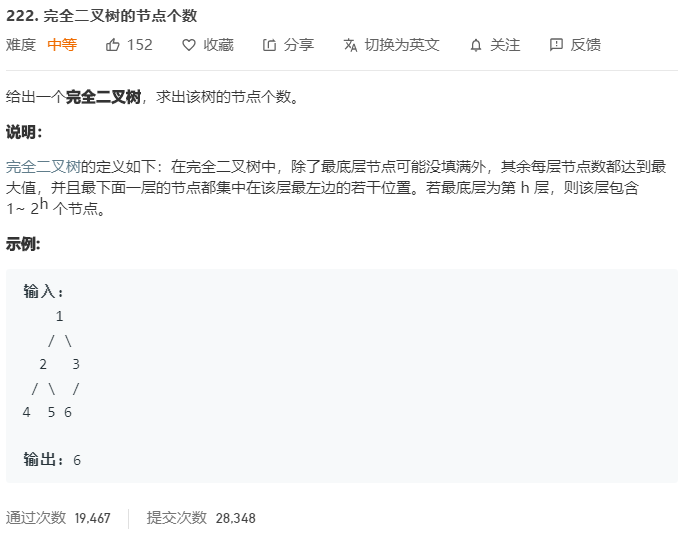
题解
二叉树结构如下:
//Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
1. 递归法
class Solution {
public:
int countNodes(TreeNode* root) {//1.递归直接统计节点数
return root? 1+countNodes(root->left)+countNodes(root->right) : 0;
}
};
2. 利用完全二叉树的性质
完满(Full)二叉树 v.s. 完全(Complete)二叉树 v.s. 完美(Perfect)二叉树
【图片来源: http://www.csie.ntnu.edu.tw/~u91029/BinaryTree2.png】
【转自https://www.cnblogs.com/idorax/p/6441043.html】
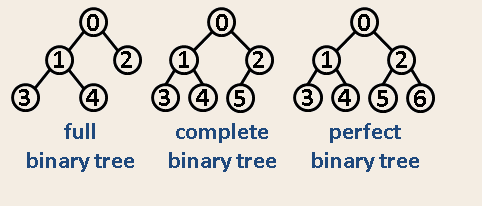
完美二叉树的节点数为$2^{n}-1$,利用这个性质可以计算完全二叉树的节点数
class Solution {
public:
int countNodes(TreeNode* root) {//2.左右分别递归,使用完全二叉树的性质
int hLeft = 0, hRight = 0;//两个变量用于计算左右高度
TreeNode *treeLeft = root, *treeRight = root;//两个指针指向左右子树
while(treeLeft){
hLeft++;
treeLeft = treeLeft->left;
}//计算最左子树高度
while(treeRight){
hRight++;
treeRight = treeRight->right;
}//右子树同上
if(hLeft == hRight) return (1<<hLeft)-1;//若左右子树高度相同,则节点数位2**n-1,用<<代替2**n
else return countNodes(root->left)+countNodes(root->right)+1;//否则就递归左右子树计算节点数
}
};
3. 利用类似二分查找的思想
如果右子树的高度等于整个树的高度减 1,说明左边都填满了,所以左子树是 perfect binary tree ,如下图。
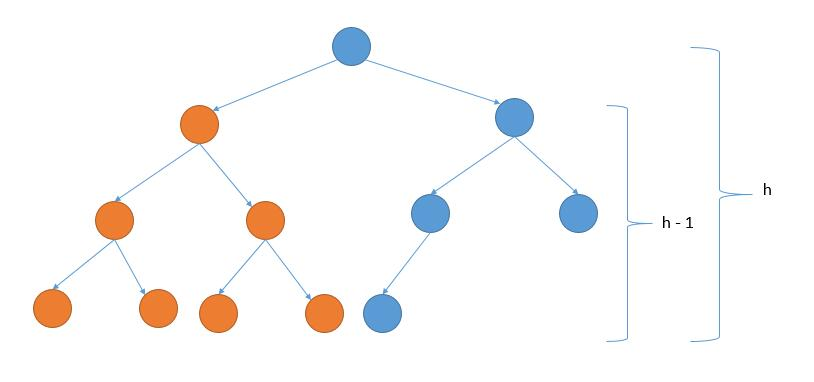
否则的话,右子树是 perfect binary tree ,如下图。
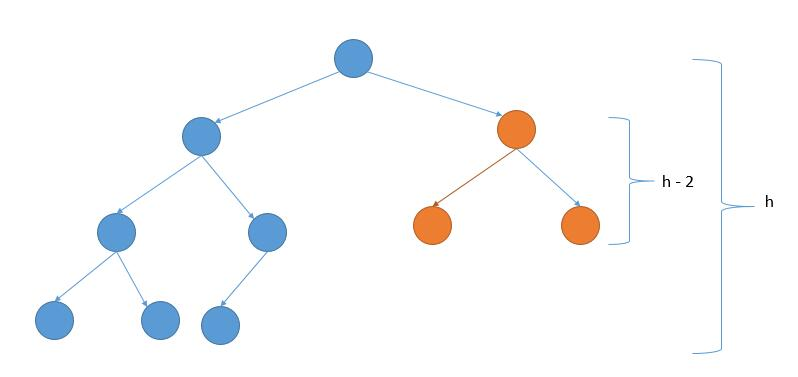
递归解法
class Solution {
public:
int getLeftHeight(TreeNode* node){
return node? 1+getLeftHeight(node->left) : -1;//递归计算z左子树深度,不算根节点,因此用-1
}
int countNodes(TreeNode* root) {//3.使用类似二分查找的思想,分别计算左右子树的节点数
int h = getLeftHeight(root);//计算左子树高度
if(h<0) return 0;//若小于0,则不存在该节点,直接返回0
if(getLeftHeight(root->right) == h-1) return (1<<h) + countNodes(root->right);//若右子树比左子树高度小1,则左子树是完美二叉树
else return (1<<h-1) +countNodes(root->left);//否则右子树是完美二叉树
}
};
非递归解法
class Solution {
public:
int getLeftHeight(TreeNode* node){
return node? 1+getLeftHeight(node->left) : -1;//递归计算z左子树深度,不算根节点,因此用-1
}
int countNodes(TreeNode* root) {//3.使用类似二分查找的思想,分别计算左右子树的节点数
int res = 0, h = getLeftHeight(root);//计算左子树高度
if(h<0) return 0;//若小于0,则不存在该节点,直接返回0
while(root){//进行二分迭代
if(getLeftHeight(root->right) == h-1){
res += (1<<h);
root = root->right;
}//右子树比左子树小1,则左子树完美,加左子树节点数,并进入右子树进行迭代
else{
res += (1<<(h-1));
root = root->left;
}//否则右子树完美,加右子树节点数,并进入左子树迭代
h--;//进入下一层h-1
}
return res;
}
};
Author ChrisHRZ
LastMod 2020-04-09