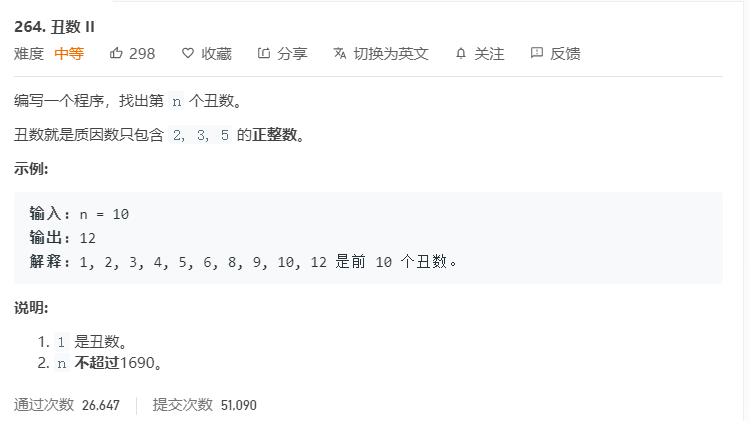
题目

题解

两个方法

1. 动态规划

就是找到丑数的生成规律，然后递推不断地生成下一个丑数，直到生成第n个丑数，需要使用三个指针，分析见注释

  • 时间复杂度$O(n)$
  • 空间复杂度$O(n)$
class Solution {//两个方法。1.动态规划
public:
    int nthUglyNumber(int n) {
        vector<int> dp(n,1);//定义一个数组存之前的丑数
        int p2=0, p3=0, p5=0;//定义三个指针，代表三个丑数当前遍历到的之前的丑数
        //遍历到第n个丑数
        //从1开始，是因为1也是丑数，占据一位
        for(int i=1; i<n; ++i){
            //丑数产生的规律是三个原始丑数（2，3，5）排列相乘
            //而下一个丑数是三个丑数与当前指针指向的丑数乘积中最小的那一个
            //这就是动态规划的状态转移公式
            dp[i] = min(2*dp[p2], min(3*dp[p3],5*dp[p5]));
            //然后看需要动哪一个原始丑数的指针
            //这里对于相等的最小丑数（如2*3==3*2，假设同时遇到这两个数）
            //两个指针都要移动，来避免数字重复出现
            if(dp[i]==2*dp[p2]) p2++;
            if(dp[i]==3*dp[p3]) p3++;
            if(dp[i]==5*dp[p5]) p5++;
        }
        return dp[n-1];//返回dp数组的最后一个，就是结果
    }
};

2. 最小堆法

使用最小堆来取最小的下一个丑数，用一个while循环来去重，这个方法要慢一点

  • 时间复杂度$O(nlog^{n})$
  • 空间复杂度$O(n)$
class Solution {//两个方法。2.最小堆法
public:
    int nthUglyNumber(int n) {
        //这里得用long，否则会溢出
        priority_queue<long, vector<long>, greater<long>> q;//建立最小堆
        q.push(1);//先压入1
        //遍历到第n个丑数
        for(int i=1; i<n; ++i){
            long tmp = q.top();q.pop();//取堆顶，即最小数
            //这个while循环是来剔除重复元素
            while(!q.empty() && tmp==q.top()){
                q.pop();
            }
            //将tmp乘以一下三个原始丑数的结果都放入最小堆
            //让最小堆来选择最小的数
            q.push(2*tmp);
            q.push(3*tmp);
            q.push(5*tmp);
        }
        return q.top();
    }
};