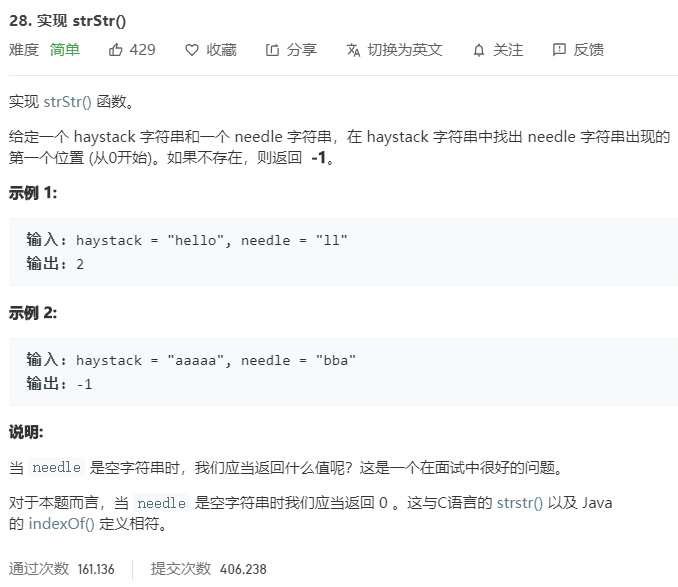
题目

题解

这道题说是简单题结果花了我两天，BF算法的确简单，但是其他的字符串匹配算法真的太复杂了。。。

1. 正则表达式

这个在leetcode上超时，未进行测试。

class Solution {
public:
    int strStr(string haystack, string needle) {
        regex r(needle);
        smatch res;
        regex_search(haystack, res, r);
        if(!res.empty()) return res.position(0);
        else return -1;
    }
};

2. 库函数法

class Solution {
public:
    int strStr(string haystack, string needle) {
        if(needle.empty()) return 0;//特殊情况，返回0
        int pos = haystack.find(needle);
        return pos;
    }
};

3. BF算法

Brute-Force算法，简称为 BF算法

  • 时间复杂度：最坏时间复杂度为 $O((N - L)L)$，最优时间复杂度为 $O(N)$。
  • 空间复杂度: $O(1)$。
class Solution {
public:
    int strStr(string haystack, string needle) {
        if(needle.empty()) return 0;//特殊情况，返回0
        int n = haystack.size();
        int m = needle.size();//计算两个的长度
        for(int i=0; i<=n-m; ++i){//两个for循环遍历两个string,注意范围到[0,n-m],字符数量不足n-m就可以停止遍历
            int j = 0;//j定义在第二个for循环外面，因为下面要判断j是否遍历到neddle末尾
            for(; j<m; ++j){
                if(haystack[i+j] != needle[j]) break;//遍历neddle，遇到不相等的字符就跳出循环
            }
            if(j == m) return i;//如果遍历到neddle末尾，就返回当前i，也就是匹配到字符串的首位
        }
        return -1;//若全部遍历完还没有匹配，说明无匹配字符串，返回-1
    }
};

4. KMP法

其效率不是很高，用的不多
该算法的详细解释可以参考阮一峰前辈的博客

  • 时间复杂度$O(M+N)$
  • 空间复杂度$O(N)$
class Solution {
public:
    vector<int> getNext(string str){
        int len = str.size();
        //定义next存储部分匹配表，每个位置存该处前缀和后缀重合的最长子串
        //注意第一个位置是-1，每一个位置的数字代表若该处不匹配子串下标跳到哪一位，因此每一位存的数是前一位数字的最长前缀和后缀匹配长度，最后一位不用存，因为最后一位匹配完成说明子串匹配完成。
        vector<int> next;
        next.push_back(-1);//先插入-1   
        int j=0, k = -1;//j是后缀，k是前缀
        while(j<len){
            //若k=-1说明又重新开时比较下一轮的子串，k跳回-1，因此j要增加一位，k跳到0
            if(k == -1 || str[j] == str[k]){
                j++;
                k++;
                next.push_back(k);
                //这时k存储的是记录的重合子串最长的长度
                //每次j和k增加都需要在next中记录该处的重合最长前后缀长度（这个需要画图理解一下）
            } else{
                k = next[k];//若出现不匹配的，k跳跃到此时next记录的该处前一位记录的的最长前缀那里
            }
        }
        return next;
    }

    int strStr(string haystack, string needle) {
        if(needle.empty()) return 0;
        int len1 = haystack.size();
        int len2 = needle.size();
        int j=0;//源串下标
        int k=0;//子串下标
        vector<int> next;
        next = getNext(needle);
        //下面这一块和getNext()函数很像，可以一起记，我会标注不同
        //其实这一块最好理解，其上下有想通的地方
        while(j<len1 && k<len2){//区别1，两个判断循环的条件
            if(k == -1 || haystack[j] == needle[k]){//区别2，对比两个字符串
                j++;
                k++;
                //区别3，不用在next中记录数了
            } else{
                k = next[k];//这个k的跳跃思想和上面类似
            }
        }
        if(k == len2) return j-k;//若遍历完是neddle遍历完成，则说明匹配成功，返回j-k，即匹配完的源串部分长度减去子串的长度
        return -1;//否则返回-1
    }
};

以下两个算法比较高效，理解起来更难一点，先占坑，回头来补

5. BM法

该算法的详细解释可以参考阮一峰前辈的博客

占坑

6. Horspool算法

BM算法的简化，详解见http://www.ifcoding.com/archives/247.html

占坑

7. SUNDAY法

该算法的理解见https://wenzhiquan.github.io/2016/05/28/2016-05-28-string-match-sunday/和http://www.ifcoding.com/archives/247.html

class Solution {
public:
    int strStr(string haystack, string needle) {
        if(needle.empty()) return 0;
        int len1 = haystack.size();
        int len2 = needle.size();
        int i=0, j=0;//源串和子串的下标
        int m = len2;//m用于存储当前匹配过程中needle相对于haystack的下一个位置
        int k = 0;//若不匹配时，k用于存此时与haystack[m]相同的最右的字符在needle中的位置
        //m和k很重要，用于跳过大部分不需要比较的字符
        while(i < len1){
            //出现不匹配的处理
            if(haystack[i] != needle[j]) {
                k = len2 - 1;
                while (k>0 && haystack[m] != needle[k]) {
                    k--;
                }//找到k
                i = m - k;//i移动到m-k处，即needle[k]在haystack里的位置
                j = 0;//j回到needle首位
                m = i + len2;//m变为现在needle的末尾在heaystack相对位置的后一位
                if (m > len1) return -1;//若此时已经超出haystack，返回-1
            }else{
                if(j == len2-1) return i-j;//若匹配到最后一位，返回匹配的第一位的位置
                i++;
                j++;
            }
        }
        return -1;
    }
};