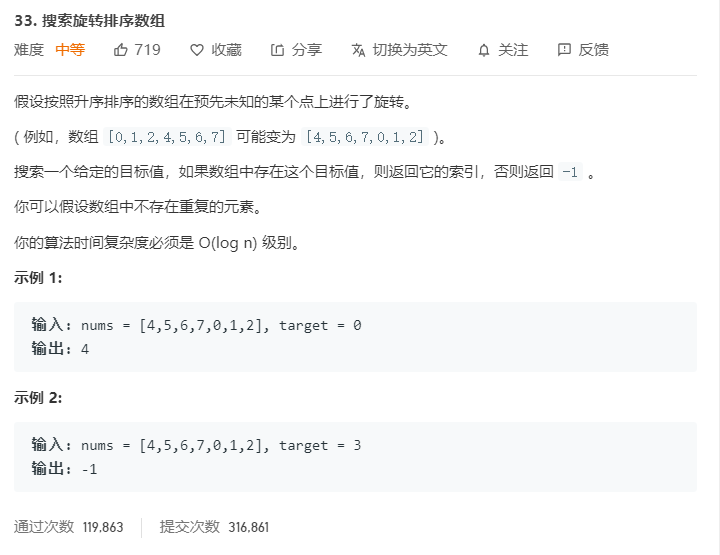
题目

题解

题目要求的复杂度一看就得联想到二分查找，这道题需要先分析一下如何二分查找，看下面的数组进行分析

  • 如果中间的数小于最右边的数，则右半段是有序的；
  • 若中间数大于最右边数，则左半段是有序的；
    我们只要在有序的半段里用首尾两个数组来判断目标值是否在这一区域内，这样就可以确定保留哪半边了
0　　1　　2　　 4　　5　　6　　7

7　　0　　1　　 2　　4　　5　　6

6　　7　　0　　 1　　2　　4　　5

5　　6　　7　　 0　　1　　2　　4

4　　5　　6　　 7　　0　　1　　2

2　　4　　5　　 6　　7　　0　　1

1　　2　　4　 　5　　6　　7　　0
  • 时间复杂度$O(logN)$
  • 空间复杂度$O(1)$
class Solution {
public:
    int search(vector<int>& nums, int target) {//修改的二分搜索法
        int left=0,right=nums.size()-1;//设置左右两个指针
        while(left<=right){//设置while循环，
            int mid=left+(right-left)/2;//设置中间值，这样写防止溢出
            if(nums[mid]==target) return mid;//若中间值与目标相等，直接返回下标
            if(nums[mid]<nums[right]){//若中间值小于右指针的值，则右半段有序
                if(nums[mid]<target && nums[right]>=target) left = mid+1;
                //用有序的右半段两边判断target是否在此区间，若在，则取该右半段
                else right = mid-1;
                //若不在，则取左半段
            }
            else{//若中间值大于右指针指，则左半段有序
                if(nums[left]<=target && nums[mid]>target) right = mid-1;
                else left = mid+1;//同上
            }
        }
        return -1;
    }
};