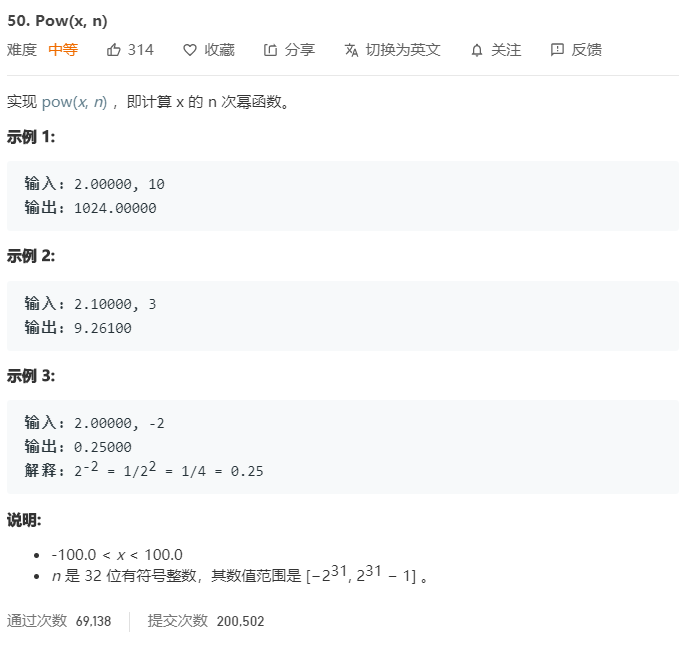
题目

题解

快速幂是指x**2n == x**n + x**n，利用这一性质，不断的一半的数进行运算。有递归法和迭代法两种，注意要区分n为奇偶和n为负数的情况。

1. 递归法

  • 时间复杂度$O(log{n})$
  • 空间复杂度$O(log{n})$
class Solution {//快速幂法。1.递归法
public:
    double myPow(double x, int n) {
        if(n == 0) return 1;//递归的末尾，所有数字的0次幂都等于0
        double half =  myPow(x,n/2);//每次取一半进行递归
        if(n%2 == 0) return half * half;//若n是偶数
        else if(n > 0) return half * half * x;//若n是奇数
        else return half * half / x; //若n是负数
    }
};

2. 迭代法

  • 时间复杂度$O(log{n})$
  • 空间复杂度$O(1)$
class Solution {//快速幂法。2.迭代法
public:
    double myPow(double x, int n) {
//快速幂是指x**2n == x**n + x**n，利用这一性质
       double res = 1;//定义res存结果
       for(int i=n; i != 0; i /= 2){//迭代从n开始，每次除以2直到0，到0就不进行操作
           if(i%2 != 0) res *= x;//关键这一步，不论什么数最后都会除到1，注意这一步要在前面
            x *= x;//这一步用来减少乘法的次数
       }
       return n<0? 1/res:res;//判断n的正负，负数的话取倒数
    }
};