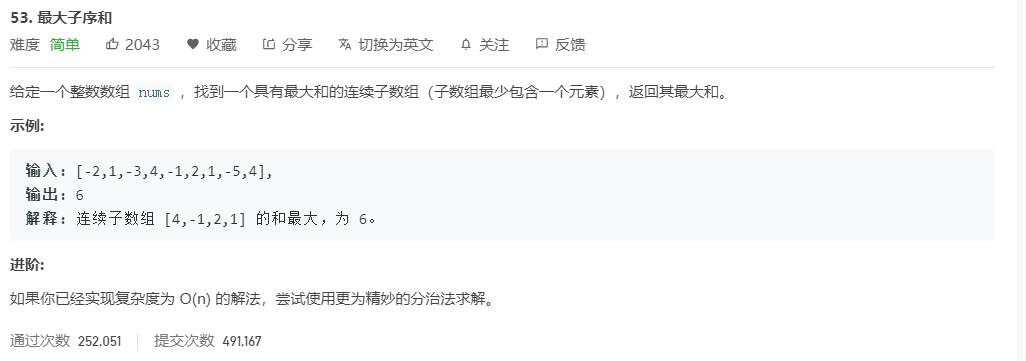
题目

题解

这题有三种解法，其中第一种暴力法肯定超时，因此主要讨论后两种方法

1. 暴力法

这个方法就是取每种情况并计算当前情况的子序和，时间复杂度达到立方，肯定超时

  • 时间复杂度$O(n^(3))$
  • 空间复杂度$O(1)$

2. 动态规划法

这个方法是时间复杂度最优也最好理解最好写的方法
思路就是存两个状态，具体看注释吧 其实这道题主要就是有负数会减小子序和

  • 时间复杂度$O(n)$
  • 空间复杂度$O(1)$
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        //动态规划法，主要维护两个个数，cur_sum(包括该元素的最大子序和),max_sum(当前存在的最大子序和)。
        //每一步选择最优方案，到全局就是全局最优方案
        int n = nums.size();
        int cur_sum = nums[0];
        int max_sum = nums[0];
        for(int i =1;i<n;i++){
            cur_sum = max(nums[i],cur_sum+nums[i]);
            max_sum = max(max_sum,cur_sum);
        }
        return max_sum;
    }
};

3. 分治法

这道题其实不适合用分治，因为除了左右两边还需要算跨过中间值的子序和，还需要用到递归增加空间复杂度，还难写
但是题目要求用分治，那就用吧

  • 时间复杂度$O(n)$
  • 空间复杂度$O(log{n})$
class Solution {//分治法
public:
    int divide(vector<int>& nums,int left, int right){
        if(left==right){
            return  nums[left];
        }//左右指针重合直接返回

        int center = left+(right-left)/2;;//取中间值

        //下面递归左右两边，分治思想
        //最后一行计算包括中间的最大子序和
        int left_sum = divide(nums,left,center);
        int right_sum = divide(nums,center+1,right);//注意center要+1，只算右边
        int cross_sum = cross_max_sum(nums,left,right,center);

        //计算上述三种分块的最大值
        int max_LR = max(left_sum,right_sum);
        return max(max_LR,cross_sum);
    }
    int cross_max_sum(vector<int>& nums,int left,int right,int center){
        if(left==right){
            return  nums[left];
        }//左右指针重合，直接返回
        //初始化四个数，左边最大值，右边最大值，左边当前和，右边当前和
        //上述四个数均包含中间数
        int left_max_sum = INT_MIN;
        int right_max_sum = INT_MIN;
        int left_cur_sum = 0;
        int right_cur_sum = 0;

        //向左右扩展计算左右的最大值，然后将左右加起来
        for(int i=center;i>=left;--i){
            left_cur_sum += nums[i];
            left_max_sum = max(left_max_sum,left_cur_sum);
        }

        for(int i=center+1;i<=right;++i){//注意center+1，避免重复
            right_cur_sum += nums[i];
            right_max_sum = max(right_max_sum,right_cur_sum);
        }
        //cout<<left_max_sum<<' '<<right_max_sum<<endl;
        return left_max_sum+right_max_sum;
    }    

    int maxSubArray(vector<int>& nums) {
        return divide(nums,0,nums.size()-1);
    }
};