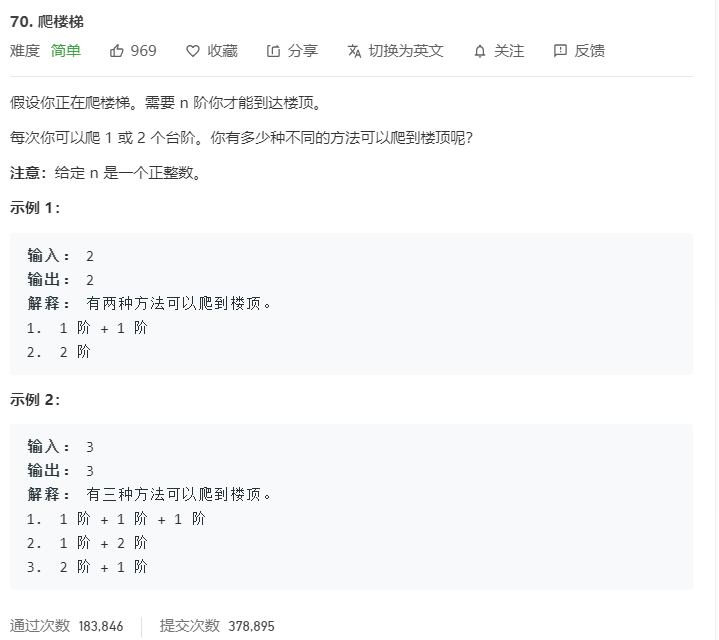
题目

题解

1. 动态规划（斐波那契数列递推公式）

其实就是斐波那契数列，可以用递推公式和通项公式求解
递推相当于动态规划，但是只和前两个数有关，所以不用存整个数组，存前两个数就可以
即当前楼梯的方法数为前两个楼梯方法数之和

  • 时间复杂度$O(n)$
  • 空间复杂度$O(1)$
class Solution {
public:

    int climbStairs(int n) {//两个方法。1. 动态规划
        int a = 1, b = 1;//a代表0位的数，即楼梯下，b代表台阶1 
        int c = 0;//这个存第三个数
        for(int i=2; i<=n; ++i){
            c = a+b;//算第三个数
            a = b;
            b = c;//更新前两个数
        }
        return b;//这个返回b，因为若n=1返回c就不对了

    }
};

2. 斐波那契通项公式

斐波那契数列的通项公式是 $$ F_n = \frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n] $$
详细的推导见这里

  • 时间复杂度$O(log(n))$，n次方的pow 方法将会用去 $log(n)$ 的时间。
  • 空间复杂度$O(1)$
class Solution {
public:
    int climbStairs(int n) {//两个方法。2. 通项公式
        double root5 = sqrt(5);
        //注意需要用n+1，
        //因为这个数列实际上是从数组下标0开始的，所以整体下标往前移动了一位，
        //第n个台阶实际上是n+1个斐波那契数列
        return (1/root5)*(pow((1+root5)/2,n+1)-pow((1-root5)/2,n+1));
    }
};

3. 递归

写法很简单，时间复杂度很高，有大量重复运算无法通过OJ，就不写了

  • 时间复杂度$O(2^n)$
  • 空间复杂度$O(n)$