题目

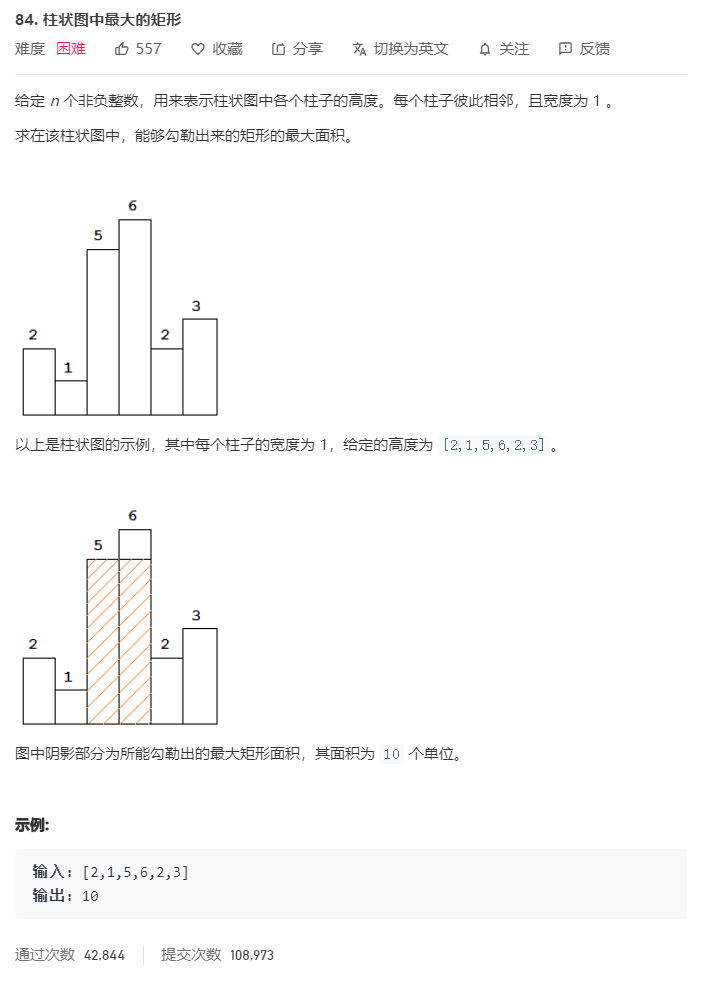
题解

1. 双数组法

  • 时间复杂度$O(N)$
  • 空间复杂度$O(N)$
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {//多种方法，可以暴力搜索，但会超时，这里用时间复杂度较低的方法。用两个主要的方法
    //1.记录左右最小矩形，求最小面积法
    //包含i处柱形图的最大矩形是左右两个小于该柱形图高度之间的宽度乘以该处柱形图的高度
    if(heights.empty()) return 0;
    int n = heights.size();
    vector<int> leftLessMin(n);
    vector<int> rightLessMin(n);
    leftLessMin[0] = -1;
    rightLessMin[n-1] = n;//定义两个数组存左右的最近的小于该处的矩形，最左和最右设置为-1和n，即两个空位置

    //存每个坐标左边的最近小矩形
    for(int i=1; i<n; ++i){
        int left = i-1;
        while(left >= 0 && heights[left] >= heights[i]){
            left = leftLessMin[left];//注意这里，若i比左边某处left的高度低，则直接找到left已经保存的左边第一个小矩形，因为left和leftLessMin[left]之间的矩形肯定大于left，同时也肯定大于i
        }
        leftLessMin[i] = left;
    }

    //存每个坐标右边边的最近小矩形
    for(int i=n-2; i>=0; --i){
        int right = i+1;
        while(right <= n-1 && heights[right] >= heights[i]){
            right = rightLessMin[right];
        }
        rightLessMin[i] = right;
    }

    int max_surface = 0;
    for(int i=0; i<n; i++){
        int area = (rightLessMin[i] - leftLessMin[i] - 1)*heights[i];//注意括号内要减一，取区间值
        max_surface = max(max_surface, area);
    }
    return max_surface;
        
    }
};

2. 用栈

  • 时间复杂度$O(N)$
  • 空间复杂度$O(N)$
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        if(heights.empty()) return 0;
        int n = heights.size();
        int maxArea = 0;
        stack<int> s;//定义栈，存每个柱状图的下标
        s.push(-1);//先存个-1作为栈顶
        for(int i=0; i<n; i++){//遍历每个柱形图
            while(s.top()!=-1 && heights[s.top()] >= heights[i]){//如果栈顶不为-1，且栈顶的的值大于当前遍历的值（有可能循环多次）
                int tmp_heights = heights[s.top()];s.pop();//取出栈顶的值
                maxArea = max(maxArea, tmp_heights*(i-s.top()-1));
                //用取出的值作为高，栈顶的值作为左边的范围，正在遍历的值作为右边的范围(开区间),计算矩形面积，并取最大
            }
            s.push(i);//计算完成继续将遍历的值压入栈，或者不符合上述循环的条件也继续压栈，即若heights继续升高也压栈
        }
        while(s.top() != -1){//遍历完成就挨个从栈中取数，计算面积
            int tmp_heights = heights[s.top()];s.pop();
            maxArea = max(maxArea, tmp_heights*(n-s.top()-1));
        }
        return maxArea;
    }
};