[Lc]94/144/145二叉树的三种遍历

题目

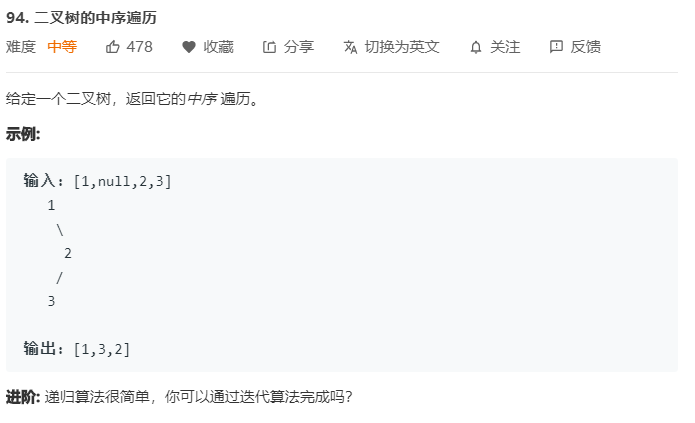
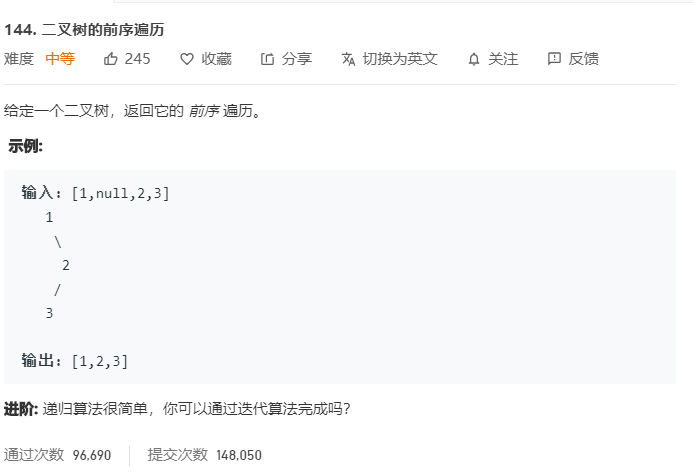
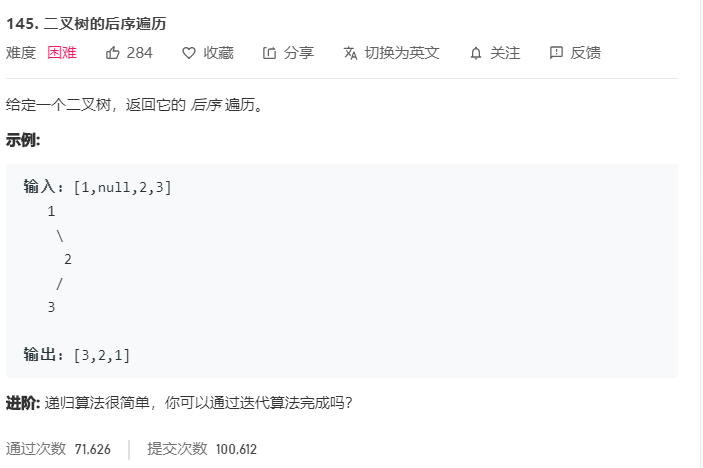
二叉树的遍历

简单地理解，满足以下两个条件的树就是二叉树：

1. 本身是有序树；
2. 树中包含的各个节点的度不能超过 2，即只能是 0、1 或者 2；

下图即一颗二叉树：

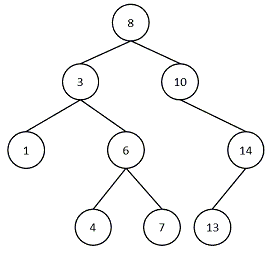
二叉树的遍历分为先序遍历，中序遍历，后续遍历，（还有层次遍历,见后文）我自己将其遍历顺序总结为：

1. 先序遍历：根->左->右
2. 中序遍历：左->根->右
3. 后序遍历：左->右->根

遍历代码

二叉树的三种遍历方式的实现有递归法，迭代法，莫里斯遍历法。递归法和迭代法都会用到栈，因此需要额外的存储空间。递归进行遍历非常简单，但是LeetCode中要求用迭代的方式实现，因此迭代和莫里斯遍历也要注意记忆。先序遍历和中序遍历可以由这三种方法严格实现，而后序遍历在使用迭代法和莫里斯遍历法时并不是严格执行，而是取巧的通过了OJ(因此后续遍历在LC上也是困难题)。这一节先将三种方法的通用代码记录下来，下一节专门讨论后序遍历。
二叉树数据结构定义如下：

// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

1. 递归法

先序遍历

class Solution {//三种方法，递归简单，先写递归。1、递归
public:
   vector<int> preorderTraversal(TreeNode* root) {
       vector<int> res;
       preorder(root,res);
       return res;
   }
   void preorder(TreeNode* cur, vector<int> &res){
       if(!cur) return;
       res.push_back(cur->val);
       preorder(cur->left,res);
       preorder(cur->right,res);
   }
};

中序遍历

class Solution {//链表，树用递归都比较简单，但递归会用栈，效率比较低。
                //题目要求写个迭代，先写递归吧
                //1、递归法
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;//设置存储结果的数组
        inorder(root,res);//调用递归函数
        return res;//返回结果
    }
    void inorder(TreeNode* root, vector<int>& res){
        if(!root) return;//若该节点为空，则直接返回
        inorder(root->left,res);//对左子树进行递归
        res.push_back(root->val);//将根节点加入res中
        inorder(root->right,res);//对右子树进行递归
    }
};

后序遍历

class Solution {//三种方法。1、递归
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        postorder(root,res);
        return res;
    }
    void postorder(TreeNode* cur, vector<int> &res){//注意用引用形参
        if(!cur) return;
        postorder(cur->left,res);
        postorder(cur->right,res);
        res.push_back(cur->val);//后序遍历的顺序
    }
};

2. 迭代法

先序遍历

class Solution {//三种方法。2、栈迭代
public:
   vector<int> preorderTraversal(TreeNode* root) {
       vector<int> res;
       if(!root) return res;//遇到特殊情况返回
       stack<TreeNode*> s;//创建栈
       auto *cur = root;//设置指针
       while(cur || !s.empty()){//只有cur指向nullptr且栈s空了才停止遍历。cur指向nullptr可能是遍历完一个子树；s空了可能回到根节点。
           if(cur){
               res.push_back(cur->val);//这是主要区别，先取值再入栈
               s.push(cur);//入栈
               cur = cur->left;
           }
           else{
               cur = s.top();s.pop();//弹出该栈顶元素
               cur = cur->right;//进入右子树
           }
       }
       return res;
   }
};

感觉用while更好理解一点，下面的方法和上面的思路一样，只是将if改为while

class Solution {//三种方法。2、栈迭代
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        if(!root) return res;//遇到特殊情况返回
        stack<TreeNode*> s;//创建栈
        auto *cur = root;//设置指针
        while(cur || !s.empty()){//只有cur指向nullptr且栈s空了才停止遍历。cur指向nullptr可能是遍历完一个子树；s空了可能回到根节点。
            while(cur){
                res.push_back(cur->val);//这是主要区别，先取值再入栈
                s.push(cur);//入栈
                cur = cur->left;
            }
            cur = s.top();s.pop();//弹出该栈顶元素
            cur = cur->right;//进入右子树
        }
        return res;
    }
};

还可以用先把右子树压入栈的方法：

class Solution {//三种方法。2、栈迭代
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        if(!root) return res;//遇到特殊情况返回
        stack<TreeNode*> s;//创建栈
        s.push(root);
        while(!s.empty()){//这样就只用s不为空就继续遍历
            auto tmp = s.top(); s.pop();
            res.push_back(tmp->val);
            if(tmp->right) s.push(tmp->right);
            if(tmp->left) s.push(tmp->left);
        }
        return res;
    }
};

中序遍历

class Solution {//链表，树用递归都比较简单，但递归会用栈，效率比较低。
                //2、迭代法，三种遍历通用
                //时间O(n)，空间O(n)和迭代一样都是栈消耗
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;//创建结果
        stack<TreeNode*> s;//创建使用的栈
        TreeNode *cur = root;//辅助指针指向根节点
        while(cur || !s.empty()){//只有cur指向nullptr且栈s空了才停止遍历。cur指向nullptr可能是遍历完一个子树；s空了可能回到根节点。
            if(cur){//若cur为存在，则将该节点压入栈，并继续遍历左子树
                s.push(cur);
                cur = cur->left;
            }
            else{//否则就可以从栈中取数存入结果，并遍历
                cur = s.top();s.pop();
                res.push_back(cur->val);
                cur = cur->right;//这一步如果cur无右子树，则返回继续从栈中取数，即返回父节点
                                 //如果cur有右子树，则进入右子树
            }
        }//若左子树为空，则存入该点，若其右子树也为空，则存入其父节点。
        return res;
    }
};

感觉用while更好理解一点，下面的方法和上面的思路一样，只是将if改为while

class Solution {//链表，树用递归都比较简单，但递归会用栈，效率比较低。
                //2、迭代法，三种遍历通用
                //时间O(n)，空间O(n)和迭代一样都是栈消耗
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;//创建结果
        stack<TreeNode*> s;//创建使用的栈
        TreeNode *cur = root;//辅助指针指向根节点
        while(cur || !s.empty()){//只有cur指向nullptr且栈s空了才停止遍历。cur指向nullptr可能是遍历完一个子树；s空了可能回到根节点。
            while(cur){//若cur为存在，则将该节点压入栈，并继续遍历左子树
                s.push(cur);
                cur = cur->left;
            }
            //否则就可以从栈中取数存入结果，并遍历
            cur = s.top();s.pop();
            res.push_back(cur->val);
            cur = cur->right;
        }//若左子树为空，则存入该店，若其右子树也为空，则存入其父节点。
        return res;
    }
};

后序遍历

注意这种方法不是严格的后序遍历，是反向后序遍历再翻转整个数组

class Solution {//三种方法。2、栈迭代
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        if(!root) return res;
        stack<TreeNode*> s;
        auto cur = root;
        while(cur || !s.empty()){
            if(cur){
                s.push(cur);//这里和先序一样，和中序不一样
                res.insert(res.begin(),cur->val);
                //主要区别，在res开头插入，即由左右中变为中右左
                cur = cur->right;//这也是区别，要注意
            }
            else{
                cur = s.top();s.pop();
                cur = cur->left;
            }
        }
        return res;
    }  
};

感觉用while更好理解一点，下面的方法和上面的思路一样，只是将if改为while

class Solution {//三种方法。2、栈迭代
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        if(!root) return res;
        stack<TreeNode*> s;
        auto cur = root;
        while(cur || !s.empty()){
            while(cur){
                s.push(cur);//这里和先序一样，和中序不一样
                res.insert(res.begin(),cur->val);
                //主要区别，在res开头插入，即由左右中变为中右左
                cur = cur->right;//这也是区别，要注意
            }
            cur = s.top();s.pop();
            cur = cur->left;//这也是区别
        }
        return res;
    }  
};

3. 莫里斯遍历法

先序遍历

记当前遍历的节点为 cur。

1. cur.left 为 null，保存 cur 的值，更新 cur = cur.right
2. cur.left 不为 null，找到 cur.left 这颗子树最右边的节点记做 pre
   2.1. pre.right 为 null，那么将 pre.right = cur，保存 cur 的值，更新 cur = cur.left
   2.2. pre.right 不为 null，说明之前已经访问过，第二次来到这里，表明当前子树遍历完成，更新 cur = cur.right

class Solution {//三种方法。3、莫里斯遍历
public:
   vector<int> preorderTraversal(TreeNode* root) {
       vector<int> res;
       if(!root) return res;//遇到特殊情况返回
       TreeNode *cur = root, *pre = nullptr;
       while(cur){//cur存在时一直遍历
           if(!cur->left){
               res.push_back(cur->val);
               cur = cur->right;
           }
           else{
               pre = cur->left;
               while(pre->right && pre->right != cur) pre = pre->right;
               if(!pre->right){
                   res.push_back(cur->val);
                   pre->right = cur;
                   cur = cur->left;
               }
               else{
                   pre->right = nullptr;
                   cur = cur->right;
               }
           }
       }
       return res;
   }
};

中序遍历

记当前遍历的节点为 cur。

1. cur.left 为 null，保存 cur 的值，更新 cur = cur.right
2. cur.left 不为 null，找到 cur.left 这颗子树最右边的节点记做 pre 2.1. pre.right 为 null，那么将 pre.right = cur，更新 cur = cur.left 2.2. pre.right 不为 null，说明之前已经访问过，第二次来到这里，表明当前子树遍历完成，保存 cur 的值，更新 cur = cur.right

class Solution {//链表，树用递归都比较简单，但递归会用栈，效率比较低。
                //2、迭代法，三种遍历通用
                //时间O(n)，空间O(n)和迭代一样都是栈消耗
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;//创建结果
        stack<TreeNode*> s;//创建使用的栈
        TreeNode *cur = root;//辅助指针指向根节点
        while(cur || !s.empty()){//只有cur指向nullptr且栈s空了才停止遍历。cur指向nullptr可能是遍历完一个子树；s空了可能回到根节点。
            if(cur){//若cur为存在，则将该节点压入栈，并继续遍历左子树
                s.push(cur);
                cur = cur->left;
            }
            else{//否则就可以从栈中取数存入结果，并遍历
                cur = s.top();s.pop();
                res.push_back(cur->val);
                cur = cur->right;
            }
        }//若左子树为空，则存入该点，若其右子树也为空，则存入其父节点。
        return res;
    }
};

后序遍历

注意这种方法不是严格的后序遍历，是反向后序遍历再翻转整个数组

//占坑，还没写

后序遍历的讨论

后序遍历有三种方法。递归法前面已经写了，这里写一个严格后序遍历的栈迭代法。
后序遍历与中序遍历的区别就在于在返回根节点时要判断是从左子树回来的还是从右子树回来的。实现方式就有

1. 用一个set存储已经遍历输出过的节点
2. 存储上一次遍历输出的节点
3. stack中push两遍值

这里写一个方法2，用的额外空间最少，其他方法有机会再补充

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> s;
        auto cur = root;
        TreeNode *last = nullptr;
        while(cur || !s.empty()){
            if(cur){
                s.push(cur);
                cur = cur->left;
            }
            else{
                TreeNode *tmp = s.top();//注意！,先暂存栈顶值
                if(tmp->right && tmp->right != last){//注意！这里是与&&条件
                //如果栈顶的节点存在右子树，且右子树没去过
                    cur = tmp->right;//进入右子树
                }
                else{//如果没有右子树，或者右子树去过了，那么就和中序遍历一样，存栈顶的值，弹出栈顶
                    res.push_back(tmp->val);//注意！这里不要转为cur
                    s.pop();
                    last = tmp;//注意！用last记录上一步遍历的值
                    //只有存值的时候标记last
                }
            }
        }
        return res;
    }
};