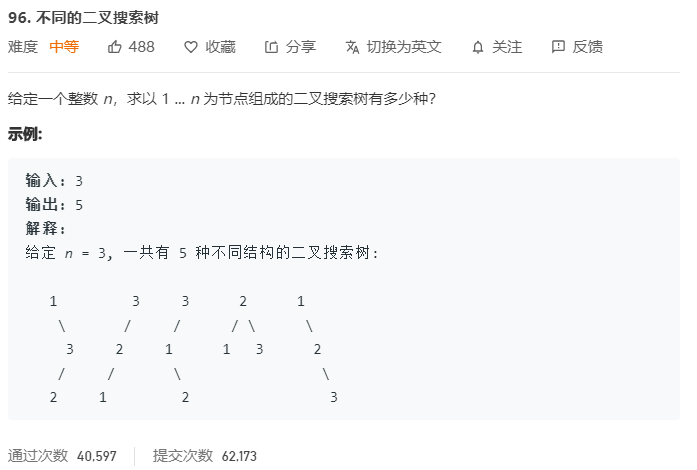
题目

题解

这道题是#95的简化版。#95要求写出所有的二叉搜索树，这道题只要求写出二叉搜索树的个数，因此要简单一点，其结题思路与卡塔兰数有关。有三种方法分别是递归、动态规划、公式法。

方法一：递归

递归方法包括一个for循环，用来遍历1~n，让每个数都作为根节点进行二叉搜索树的建立。然后对其左右子树进行递归，计算其左右子树的二叉搜索树的排列组合数量。
注意如果直接递归无法通过OJ，会超时。采用unordered_map先将每个n对应下的结果进行记录，就可以减少大量重复计算通过OJ。

class Solution {//三种方法。1、递归。时间复杂度O(n)，空间复杂度O(1),但是递归要用栈，需要额外的空间。
//直接递归的方法会超时，无法通过OJ，用memo记住运算结果可以减少运算量
unordered_map<int,int> memo;//注意直接写到私有变量里，写到程序里会出错
public:
    int numTrees(int n) {
        if(n==0 || n==1){
            return 1;
        }//特殊情况的判断，只有0和1个数时直接返回1
        return getRes(n);
    }
    int getRes(int n){
        if(memo.count(n)) return memo[n];
        //如果已经计算过n下的值，直接返回结果，减少计算量
        if(n==0 || n==1){
            return 1;
        }
        int res = 0;//设置res用于累加结果
        for(int i=1;i<=n;i++){//数组是1~n，i表示为根的数
            int leftTreeNum = getRes(i-1);//左子树的排列组合数量
            int rightTreeNum = getRes(n-i);//右子树的排列组合数量
            res += leftTreeNum*rightTreeNum;
            //二者相乘即以i为根的二叉搜索树数量
        }
        memo[n] = res;
        return res;//返回结果
    }
};

方法二：动态规划

一般的递归都可以转化为动态规划，但递归是top-down，动态规划是bottom-up。递归是通过不断地压栈，直到n为0或1时进行出栈，一直返回到顶层输出结果。动态规划的思路与加入memo的递归类似，对于长度一样的数组,如[1,2,3],[6,7,8],其二叉搜索树的排列组合数量是一致的，只与数组的长度有关。因此我们维护一个数组dp，求出n为0,1,2…n的结果并存储，最终返回dp[n]。
动态规划法需要两个循环，一个外循环用于遍历1~n，计算dp[1]~dp[n]；内循环和递归一样首先以不同的数为根节点，其次利用左右子树的排列组合数量相乘得到以该节点为根的二叉搜索树的数量，最后叠加上不同的节点为根的结果得到dp[n]。

class Solution {//三种方法。2、动态规划。时间复杂度O(n**2)，空间复杂度O(n)
public:
    int numTrees(int n) {
        if(n==0 || n==1) return 1;//特殊情况
        //int dp[n+1];//因为有累加，使用静态数组有问题，最好用动态数组
        vector<int> dp(n+1);//vector<int>的初始化值默认为0
        //注意这里要用n+1初始化，因为其下标从0开始
        dp[0]=1;
        dp[1]=1;
        for(int len=2; len<=n; ++len){
            for(int i=1; i<=len; ++i){
                int left = i-1;
                int right = len-i;
//注意这两句与递归不同，这里是获得左右节点的数量而不是二叉搜索树的数量
                dp[len] += dp[left]*dp[right];
            }
        }
        return dp[n];
    }
};

方法三：公式法

这道题实际上就是求卡塔兰数的值，直接通过递推公式得到结果。递推公式如下： 

class Solution {
public:
    int numTrees(int n) {//三种方法。3、公式法
        if(n==0 || n==1) return 1;//特殊情况
        long C = 1;//首项，注意用long，否则会溢出
        for(int i=0;i<n;i++){
            C = C*2*(2*i+1)/(i+2);//根据递推公式计算
        } 
        return C;
    }
};